Question

已知F₁、F₂分别是双曲线C：

x2

4

-

y2

5

=1的左、右焦点，点A在双曲线C上，点M（1，0）．若AM平分∠F₁AF₂，则|AM|=

2

6

．

Answer 1

分析：首先求出双曲线

x2

4

-

y2

5

=1的半焦距c=3，可得左焦点F₁（-3，0），右焦点F₂（3，0），求出|MF₁|=4，|MF₁|=2．再利用三角形内角平分线定理，在△F₁AF₂中根据AM平分∠F₁AF₂，得

AF 1

AF 2

=

MF1

MF2

=2，所以|AF₁|=2|AF₂|，结合双曲线的定义得|AF₁|-|AF₂|=2a=4，从而有|AF₁|=8，|AF₂|=4，最后分别在△F₁AF₂中和△MAF₂中利用余弦定理，可得|AM|²=24，从而得到|AM|=2

6

．

解答：解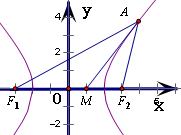：∵双曲线C的方程为

x2

4

-

y2

5

=1
∴c²=4+5=9，c=3，可得左焦点F₁（-3，0），右焦点F₂（3，0），
因此|MF₁|=1+3=4，|MF₁|=3-1=2，
∵△F₁AF₂中，AM平分∠F₁AF₂，
∴

AF 1

AF 2

=

MF1

MF2

=2，可得|AF₁|=2|AF₂|
又∵点A在双曲线C上，|AF₁|-|AF₂|=2a=4
∴|AF₁|=8，|AF₂|=4
∴△F₁AF₂中，cos∠F₁F₂A=

62+42-82

2×6×4

=-

1

4

所以在△MAF₂中，|AM|²=2²+4²-2×2×4cos∠F₁F₂M=24
∴|AM|=

24

=2

6

故答案为：2

6

点评：本题给出双曲线的焦点三角形F₁AF₂中，角A的平分线恰好经过点M（1，0），求线段AM的长度，着重考查了双曲线的简单性质、三角形内角平分线定理和余弦定理等知识点，属于中档题．