题目内容
如图，]
四棱锥P—ABCD中面PDC⊥面ABCD，底面为边长等于1的正方形，△PCD为正三角形，求
与面PBC所成的角.
解：以D为坐标原点，以DA、DC所在的直线为x轴，y轴，过D作面DCA的垂线为z轴，建立空间直角坐标系，则P（0，，
），A（1，0，0），B（1，1，0），C（0，1，0），取面PBC的法向量n=(x,y,z),则有n·
=0,且n·
=0，即x+
-
z=0且-x=0,令z=1,可得y=
,x=0,故n=(0,
,1).又
=（-1，
，
），所以
·n=0+
+
=
,
又|
|=
，|n|=2,
∴cos〈
,n〉=
.
∴PA与面PBC所成的角为
-arccos
.
练习册系列答案
相关题目
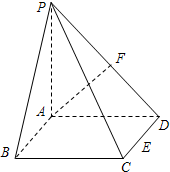20、如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，且PA=AD，点F是棱PD的中点，点E在棱CD上移动．
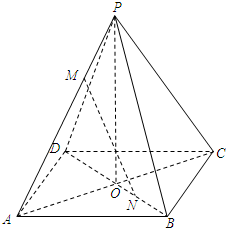如图，正四棱锥P-ABCD中，PA=AB，点M，N分别在PA，BD上，且
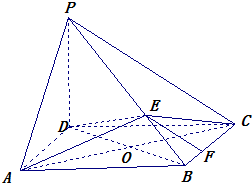如图，在四棱锥P-ABCD中，PD⊥平面ABCD，四边形ABCD是菱形，AC=6
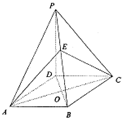（2013•婺城区模拟）如图，在四棱锥P-ABCD中，PD⊥平面ABCD，底面ABCD是菱形，∠BAD=60°，O为AC与BD的交点，E为PB上任意一点．
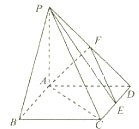（2013•蓟县一模）如图，在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，且PA=AD点F是棱PD的中点，点E为CD的中点．