题目内容
已知a，b∈（0，2]，函数f(x)=
(asint-2bcost)dt在[
，
]上为增函数的概率是（ ）
| ∫ | x 1 |
| π |
| 4 |
| π |
| 3 |
分析：先积分求出f（x）的表达式，再由f（x）在[
，
]上为增函数，导数在区间[
，
]上大于等于0恒成立．求出满足a，b的关系式，最后把a看成横轴，b看成纵轴，a，b在一象限围成边长为2的正方形的面积为总的基本事件，a，b关系式与正方形围成的面积为满足条件的基本事件，用面积之比求出概率．
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
解答：解：∵f(x)=
=(-acosx-2bsinx)-(-acos1-2bsin1)，
∴f'（x）=asinx-2bcosx．
若f′（x）≥0在区间[
，
]上恒成立，则函数f（x）在区间[
，
]是增函数．
∵sinx，cosx在区间[
，
]上均大于0，
∴asinx≥2bcosx，
≥
，即
≤tanx．
∴f′（x）≥0在区间[
，
]上恒成立?[tanx]min＞
，x∈[
，
]．
∵tanx在[
，
]上的最小值为tan
=1，∴
≤1，b≤
a．
如图所示：函数f（x）在区间[
，
]上为增函数的概率为P=
=
．
故选A．
| (-acost-2bsint) | | x 1 |
∴f'（x）=asinx-2bcosx．
若f′（x）≥0在区间[
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
∵sinx，cosx在区间[
| π |
| 4 |
| π |
| 3 |
∴asinx≥2bcosx，
| sinx |
| cosx |
| 2b |
| a |
| 2b |
| a |
∴f′（x）≥0在区间[
| π |
| 4 |
| π |
| 3 |
| 2b |
| a |
| π |
| 4 |
| π |
| 3 |
∵tanx在[
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
| 2b |
| a |
| 1 |
| 2 |
如图所示：函数f（x）在区间[
| π |
| 4 |
| π |
| 3 |
| ||
| 2×2 |
| 1 |
| 4 |
故选A．
点评：由已知正确求出a、b满足的关系式是解题的关键．另外转化思想是解此类问题常用方法之一．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在
上为增函数的概率是
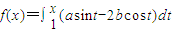在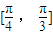
上为增函数的概率是（ ）
