题目内容
3.已知x>0,y>0,2x+y=2,则xy的最大值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{4}$ |
分析 利用基本不等式的性质即可得出.
解答 解:∵x>0,y>0,且2x+y=2,
∴xy=$\frac{1}{2}$(2x•y)≤$\frac{1}{2}$($\frac{2x+y}{2}$)2=$\frac{1}{2}$,当且仅当x=$\frac{1}{2}$,y=1时取等号,
故则xy的最大值为$\frac{1}{2}$,
故选:A
点评 熟练掌握基本不等式的性质是解题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
14.已知集合A={ x|-2<x<6},B={ x|4<x<7},则A∩B=( )
| A. | {4,5,6} | B. | {5} | C. | (-2,7) | D. | (4,6) |
8.在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为( )
| A. | (-2,-1) | B. | (-1,0) | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
13.下列说法正确的是( )
| A. | a∈R,“$\frac{1}{a}$<1”是“a>1”的必要不充分条件 | |
| B. | “p∨q为真命题”的必要不充分条件是“p∧q为真命题” | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| D. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 |
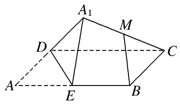 如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)
如图,矩形ABCD中,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻转过程中,下列说法正确的是①②.(填序号)