题目内容
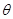 是三角形的一个内角,且
是三角形的一个内角,且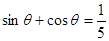 ,则方程
,则方程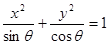 所表示的曲线为( ).
所表示的曲线为( ).
A.焦点在 轴上的椭圆 轴上的椭圆 | B.焦点在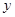 轴上的椭圆 轴上的椭圆 |
C.焦点在 轴上的双曲线 轴上的双曲线 | D.焦点在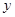 轴上的的双曲线 轴上的的双曲线 |
C
解析考点:双曲线的标准方程;椭圆的标准方程.
分析:把 sinθ+cosθ=  两边平方可得,sinθ?cosθ="-"
两边平方可得,sinθ?cosθ="-" 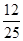 <0,可判断θ为钝角,cosθ<0,从而判断方程所表示的曲线.
<0,可判断θ为钝角,cosθ<0,从而判断方程所表示的曲线.
解:因为θ∈(0,π),且sinθ+cosθ= ,所以,θ∈(
,所以,θ∈( 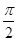 ,π),
,π),
且|sinθ|>|cosθ|,所以θ∈(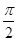 ,
,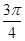 ),从而cosθ<0,
),从而cosθ<0,
从而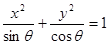 表示焦点在x轴上的椭圆.
表示焦点在x轴上的椭圆.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设θ是三角形的一个内角,且sinθ+cosθ=
,则方程x2sinθ-y2cosθ=1表示的曲线是( )
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在x轴上的椭圆 |
| C、焦点在y轴上的双曲线 |
| D、焦点在y轴上的椭圆 |
θ是三角形的一个内角,且sinθ+cosθ=
,则方程
+
=1所表示的曲线为( )
| 1 |
| 5 |
| x2 |
| sinθ |
| y2 |
| cosθ |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |