题目内容
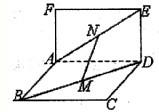 如图,空间中两个有一条公共边AD的正方形ABCD和ADEF.设M、N分别是BD和AE的中点,那么
如图,空间中两个有一条公共边AD的正方形ABCD和ADEF.设M、N分别是BD和AE的中点,那么①AD⊥MN;②MN∥平面CDE;
③MN∥CE;④MN、CE异面
以上4个命题中正确的是
①②③
①②③
.分析:①是考查了线线垂直,而证明线线垂直常用先证线面垂直再通过线面垂直得到线线垂直.
②是考查了线面平行,而证明线面平行常用先证线线平行再得到线面平行,或面面平行得到线面平行.
③线线平行的判定可通过中位线定理,平行四边形和梯形的性质得到或通过线面平行得到线线平行.
②是考查了线面平行,而证明线面平行常用先证线线平行再得到线面平行,或面面平行得到线面平行.
③线线平行的判定可通过中位线定理,平行四边形和梯形的性质得到或通过线面平行得到线线平行.
解答:
解:(1)取AD的中点H,连接NH,MH则NH
DE,MH
CD
又AD⊥DE,AD⊥CD所以AD⊥NH,AD⊥MH又NH∩MH=H 所以AD⊥面MHN 所以AD⊥MN 所以(1)正确
(2)由(1)知NH
DE,MH
CD 则面MHN∥面CDE 又MN?面MHN 所以MN∥平面CDE 所以(2)正确
(3)连接AC则AC过点M 在三角形ACE中M,N为中点所以MN∥CE 所以(3)正确,(4)错
故答案为:①②③

解:(1)取AD的中点H,连接NH,MH则NH
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
又AD⊥DE,AD⊥CD所以AD⊥NH,AD⊥MH又NH∩MH=H 所以AD⊥面MHN 所以AD⊥MN 所以(1)正确
(2)由(1)知NH
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
(3)连接AC则AC过点M 在三角形ACE中M,N为中点所以MN∥CE 所以(3)正确,(4)错
故答案为:①②③
点评:此题主要考查了空间中线与线,线与面的位置关系,要准确的把握线面间的关系需要对线面垂直,线面平行,面面垂直的判定定理和性质定理要准确理解和记忆,因为这是我们解决这一类问题的依据!

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目


 如图,空间中两个有一条公共边AD的正方形ABCD和ADEF.设M、N分别是BD和AE的中点,那么
如图,空间中两个有一条公共边AD的正方形ABCD和ADEF.设M、N分别是BD和AE的中点,那么