题目内容
若向量
=（2，x+1），
=（x+2，6），又，的夹角为锐角，则实数x的取值范围为 ________．
{x|x＞-
，且x≠2}
分析：利用向量的数量积的公式得到要使向量的夹角是锐角需数量积大于0但不同向；利用向量的数量积公式得到不等式，利用向量共线的充要条件列出方程求出x的范围．
解答：
的夹角为锐角，
所以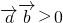
但不同向
∵
=8x+10
∴8x+10＞0解得
当同向时，存在λ＞0使
即
解得x=2
故答案为{x|x＞-且x≠2}
点评：本题考查向量的数量积表示向量的夹角、向量共线的充要条件．
，且x≠2}分析：利用向量的数量积的公式得到要使向量的夹角是锐角需数量积大于0但不同向；利用向量的数量积公式得到不等式，利用向量共线的充要条件列出方程求出x的范围．
解答：
的夹角为锐角，所以
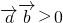但不同向∵
=8x+10∴8x+10＞0解得
当
同向时，存在λ＞0使即
解得x=2故答案为{x|x＞-
且x≠2}点评：本题考查向量的数量积表示向量的夹角、向量共线的充要条件．
练习册系列答案
阅读快车系列答案
相关题目
已知向量p=（2，x-1），q=（x，-3），且p⊥q，若由x的值构成的集合A满足A?{x|ax=2}，则实数a构成的集合是（ ）
| A、{0} | ||
B、{
| ||
| C、空集 | ||
D、{0，
|
=（x-1，2-y）向量
=（y-2，x-1），若
∥
，则x2+y2= ．
=（x-1，2-y）向量
=（y-2，x-1），若
∥
，则x2+y2= ．