Question

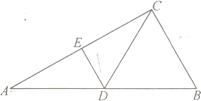
【题目】如图，已知，两个城镇相距20公里，设是中点，在的中垂线上有一高铁站，的距离为10公里．为方便居民出行，在线段上任取一点（点与，不重合）建设交通枢纽，从高铁站铺设快速路到处，再铺设快速路分别到，两处．因地质条件等各种因素，其中快速路造价为3百万元/公里，快速路造价为2百万元/公里，快速路造价为4百万元/公里， 设，总造价为（单位：百万元）．

（1）求关于的函数关系式，并指出函数的定义域；

（2）求总造价的最小值，并求出此时的值．

Answer 1

【答案】（1），定义域；（2）最小值为（百万元），此时．

【解析】

(1)根据题意有,,因此根据不同地段的造价即可列出关于的函数关系式,再求出定义域即可;

(2)根据(1)中结论可设,利用导数求出函数的单调性及其最大值,从而可得出结论.

(1)∵,,,

∴,,,

∴

，定义域；

(2)设,

则,

令,又,所以,

当,,单调递减;

当,,单调递增;

所以的最小值为,

所以的最小值为(百万元),此时.