题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
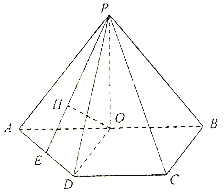
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
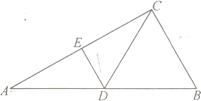
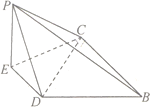
如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(1)见解析;(2)直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】
(1)在题图1中,可证![]() ,在题图2中,
,在题图2中,![]() 平面
平面![]() .进而得到
.进而得到![]() 平面
平面![]() .从而证得平面
.从而证得平面![]() 平面
平面![]() ;
;
(2)可证得![]() 平面
平面![]() .
. ![]() .则以
.则以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立如图所示的空间直角坐标系,利用空间向量可求直线
轴的正方向建立如图所示的空间直角坐标系,利用空间向量可求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:在题图1中,因为![]() ,且
,且![]() 为
为![]() 的中点.由平面几何知识,得
的中点.由平面几何知识,得![]() .
.
又因为![]() 为
为![]() 的中点,所以
的中点,所以![]()
在题图2中,![]() ,
,![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)解:因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
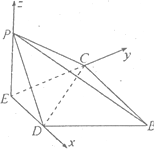
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立如图所示的空间直角坐标系
轴的正方向建立如图所示的空间直角坐标系
在题图1中,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则 ,即
,即![]()
令![]() ,则
,则![]() .所以
.所以![]() .
.
设![]() 与
与![]() 平面所成的角为
平面所成的角为![]() ,
,
则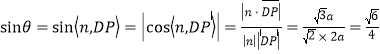 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.