题目内容
已知椭圆 的离心率
的离心率 ,连接椭圆的四个顶点得到的菱形的面积为
,连接椭圆的四个顶点得到的菱形的面积为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)圆x2+y2=1的一条切线l与椭圆C相交于A,B两点,问是否存在上述直线l使 成立?若存在,求出直线l的方程;若不存在,请说明理由.
成立?若存在,求出直线l的方程;若不存在,请说明理由.
解:(Ⅰ)由 ,得a2=4c2,再由c2=a2-b2,解得a=
,得a2=4c2,再由c2=a2-b2,解得a= b①.
b①.
由连接椭圆的四个顶点得到的菱形的面积为 ,可知2ab=4
,可知2ab=4 ②.
②.
①②可得a=2,b= .
.
所以椭圆的方程为 .
.
(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1
当方程为x=1时,直线l与椭圆的交点为A(1, ),B(1,-
),B(1,- ),则
),则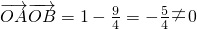
同理方程为x=1时, 也不成立;
也不成立;
②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,
直线方程代入椭圆方程,消去y,可得(3+4k2)x2+8kmx+4m2-12=0
设A(x1,y1),B(x2,y2),则x1+x2=-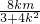 ,x1x2=
,x1x2=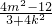
∴y1y2=(kx1+m)(kx2+m)=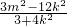
∴ =x1x2+y1y2=
=x1x2+y1y2=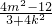 +
+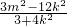 =
=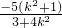 <0
<0
综上所述,直线l不存在.
分析:(Ⅰ)由 ,得a2=4c2,再由c2=a2-b2,解得a=
,得a2=4c2,再由c2=a2-b2,解得a= b,利用连接椭圆的四个顶点得到的菱形的面积为
b,利用连接椭圆的四个顶点得到的菱形的面积为 ,即可求得椭圆的方程;
,即可求得椭圆的方程;
(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1,可得 不成立;
不成立;
②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,直线方程代入椭圆方程,利用韦达定理,结合向量的数量积运算,即可得到结论.
点评:本题考查椭圆的标准方程,考查直线与圆,直线与椭圆的位置关系,考查向量的数量积运算,属于中档题.
 ,得a2=4c2,再由c2=a2-b2,解得a=
,得a2=4c2,再由c2=a2-b2,解得a= b①.
b①.由连接椭圆的四个顶点得到的菱形的面积为
 ,可知2ab=4
,可知2ab=4 ②.
②.①②可得a=2,b=
 .
.所以椭圆的方程为
 .
.(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1
当方程为x=1时,直线l与椭圆的交点为A(1,
 ),B(1,-
),B(1,- ),则
),则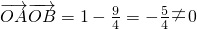
同理方程为x=1时,
 也不成立;
也不成立;②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,
直线方程代入椭圆方程,消去y,可得(3+4k2)x2+8kmx+4m2-12=0
设A(x1,y1),B(x2,y2),则x1+x2=-
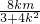 ,x1x2=
,x1x2=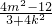
∴y1y2=(kx1+m)(kx2+m)=
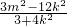
∴
 =x1x2+y1y2=
=x1x2+y1y2=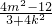 +
+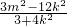 =
=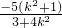 <0
<0综上所述,直线l不存在.
分析:(Ⅰ)由
 ,得a2=4c2,再由c2=a2-b2,解得a=
,得a2=4c2,再由c2=a2-b2,解得a= b,利用连接椭圆的四个顶点得到的菱形的面积为
b,利用连接椭圆的四个顶点得到的菱形的面积为 ,即可求得椭圆的方程;
,即可求得椭圆的方程;(Ⅱ)假设存在直线l满足条件
①当直线l的斜率不存在时,则方程为x=±1,可得
 不成立;
不成立;②斜率存在时,假设方程为y=kx+m,由直线与圆相切可得m2=1+k2,直线方程代入椭圆方程,利用韦达定理,结合向量的数量积运算,即可得到结论.
点评:本题考查椭圆的标准方程,考查直线与圆,直线与椭圆的位置关系,考查向量的数量积运算,属于中档题.

练习册系列答案
相关题目

 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程; ,
, ,
, 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切.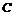 的方程;
的方程; ,
, ,
,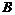 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.