Question

数列{a_n}是等比数列,项数是偶数,各项为正,它所有项的和等于偶数项和的4倍,且第二项与第四项的积是第三项与第四项和的倍,

(1)求{a_n}的通项公式;

(2)证明{lga_n}成等差数列;

(3)问数列{lga_n}的前几项和最大.

Answer 1

(1)解:由题意知q≠1,且=

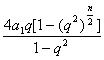,即=1,∴q=.又a₁q·a₁q³=(a₁q²+a₁q³),∴a₁=81.

a_n=81×()^n-1=()^n-5.

(2)证明:lga_n+1-lga_n=lg()^n-4-lg()^n-5=lg,

∴{lga_n}成等差数列.

(3)解:设数列{a_n}的前n项和最大,则有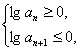

    即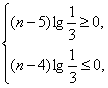解得4≤n≤5.

∴数列{lga_n}的前4项或前5项和最大.