Question

如图，正三棱柱ABC—A₁B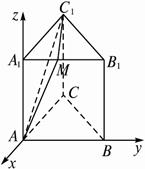₁C₁的底面边长为a,侧棱长为2a,求AC₁与侧面AB₁所成的角.

Answer 1

解法一：建立如上图所示的空间直角坐标系，则A（0，0，0），B（0，a,0），A₁（0，0，a），C₁（-a,,a）,取A₁B₁中点M，则M（0，,a）,连结AM，MC₁，有=(-a,0,0),=(0,a,0),∴=(0,0,a).由于·=0，·=0，所以MC₁⊥面AB₁，∴∠C₁AM是AC₁与侧面AB₁所成的角θ.?

∵=(-a, ,a),AM=(0, ,a),?

∴·=0++2a²=.?

而||==a,| |==a,?

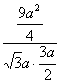∴cos〈·〉==.∴〈·〉=30°,?

即AC₁与侧面AB₁所成的角为30°.

解法二：（法向量法）：（同解法一）=（0，0，a）.设侧面A₁B的法向量n=(λ,x,y),所以n·=0，且n·=0，∴ax=0,且ay=0,∴x=y=0,故n=(λ,0,0).?

∵=(-,,a).

∴cos〈,n〉===-.?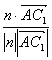

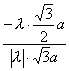∴sinθ=|cos〈,n〉|=,∴θ=30°.

点评：充分利用图形的几何特征建立适当的空间直角坐标系，再用向量有关知识求解线面角.解法二给出了一般的方法，先求平面法向量与斜线夹角，再进行转换.