题目内容

方程|x|（x-1）-k=0有三个不相等的实根，则k的取值范围是

A.
$数学公式$
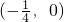
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

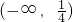
A
分析：将方程转化为函数y=k与y=|x|（x-1），将方程要的问题转化为函数图象交点问题．
解答：

解：如图，作出函数y=|x|•（x-1）的图象，
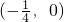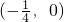由图象知当k∈ $\text{[math]}$ 时，函数y=k与y=|x|（x-1）有3个不同的交点，
即方程有3个实根．
故选A．
点评：本题研究方程根的个数问题，此类问题首选的方法是图象法即构造函数利用函数图象解题，其次是直接求出所有的根．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

函数f（x）=x•e^x在点（1，e）处的切线方程为（　　）

（1）已知矩阵A=

a	2
1	b

有一个属于特征值1的特征向量

，
①求矩阵A；
②已知矩阵B=

1	-1
0	1

，点O（0，0），M（2，-1），N（0，2），求△OMN在矩阵AB的对应变换作用下所得到的△O'M'N'的面积．
（2）已知在直角坐标系xOy中，直线l的参数方程为

（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，曲线C的极坐标方程为ρ²-4ρco sθ+3=0．
①求直线l普通方程和曲线C的直角坐标方程；
②设点P是曲线C上的一个动点，求它到直线l的距离的取值范围．
（3）已知函数f（x）=|x-1|+|x+1|．
①求不等式f（x）≥3的解集；
②若关于x的不等式f（x）≥a²-a在R上恒成立，求实数a的取值范围．

已知函数f(x)=ln(x+1)-

（1）求f（x）的单调区间；
（2）求曲线y=f（x）在点（1，f（1））处的切线方程；
（3）求证：对任意的正数a与b，恒有lna-lnb≥1-

已知二次函数f（x）=ax²+bx+c（a，b，c为常数）满足条件：①图象过原点；②f（1+x）=f（1-x）；③方程f（x）=x有两个相等的实根．
（1）求f（x）的解析式；
（2）求f（x）在x∈[-1，2]的值域．

已知函数f(x)=

x2+(a+1)x+2ln(x-1)．
（Ⅰ）若曲线y=f（x）在点（2，f（2））处的切线与直线2x-y+1=0平行，求出这条切线的方程；
（Ⅱ）讨论函数f（x）的单调区间；
（Ⅲ）若对于任意的x∈（1，+∞），都有f（x）＜-2，求实数a的取值范围．