题目内容
已知![]() ,且
,且![]()
(1)求![]() ,
,![]() 的表达式,猜想
的表达式,猜想![]()
![]() 的表达式并用数学归纳法证明;
的表达式并用数学归纳法证明;
(2)若关于![]() 的函数
的函数![]() 在区间(-
在区间(-![]() ,-1]上的最小值为12,求
,-1]上的最小值为12,求![]() 的值。
的值。
解:(1)∵![]() ,∴
,∴![]() ,
,![]() ,∴猜想
,∴猜想![]()
证明:①当![]() 时,
时,![]() 成立;
成立;
②假设![]() 时,表达式成立,即
时,表达式成立,即![]() ,
,
则当![]() 时,
时,![]()
∴当![]() 时,表达式成立
时,表达式成立
由①②得对任意![]() ,
,![]()
(2)∵![]() ,∴
,∴![]() ,
,
∴![]() 。
。
①当![]() 即
即![]() 时,函数
时,函数![]() 在区间(-
在区间(-![]() ,-1]上是减函数
,-1]上是减函数
∴当![]() 时,
时,![]() 即
即![]() ,
,
又![]() ,∴该方程没有整数解;
,∴该方程没有整数解;
②当![]() ,即
,即![]() 时,
时,![]()
∴![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
综上所述,![]() 为所求的值
为所求的值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,且
,且 .
. ;
; .
. ,
, 且
且
 的周期;
的周期;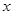 的值;
的值; 且
且
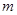 的值;(2)判定
的值;(2)判定 的奇偶性;
的奇偶性;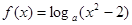 , 且
, 且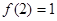 .
. 的值;
(2)求
的值;
(2)求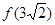 的值;(3)解不等式
的值;(3)解不等式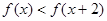 .(10分)
.(10分)