题目内容
已知正三角形ABC的边长为1，点P是AB边上的动点，点Q是AC边上的动点，且
，则
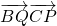的最大值为
- A.
- B.
- C.
- D.
D
分析：利用向量的运算法则和数量积即可化为关于λ的二次函数，利用二次函数的单调性即可得出最大值．
解答：如图所示，
=
=
=
-
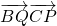+（λ-1）
+
=（λ-λ2+1）×1×1×cos60°-λ+λ-1
=
=
，（0≤λ≤1）．
当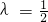
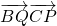时，则的最大值为．
故选D．
点评：熟练掌握向量的运算法则和数量积的运算性质、二次函数的单调性是解题的关键．
分析：利用向量的运算法则和数量积即可化为关于λ的二次函数，利用二次函数的单调性即可得出最大值．
解答：如图所示，
==
=
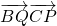-+（λ-1）+=（λ-λ2+1）×1×1×cos60°-λ+λ-1
=
=
，（0≤λ≤1）．当
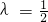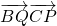时，则的最大值为．故选D．
点评：熟练掌握向量的运算法则和数量积的运算性质、二次函数的单调性是解题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知正三角形ABC的边长为a，那么三角形ABC根据斜二测画法得到的平面直观图三角形A′B′C′的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知正三角形ABC的边长为1，且
=
，
=
，则|
-
|=（ ）
| BA |
| a |
| AC |
| b |
| a |
| b |
A、
| ||
| B、3 | ||
C、
| ||
| D、1 |
如图，已知正三角形ABC的边长为2，点D为边AC的中点，点E为边AB上离点A较近的三等分点，则