Question

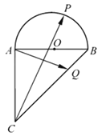
【题目】如图，在等腰直角三角形ABC中，∠CAB＝90°，AB＝2，以AB为直径在△ABC外作半圆O，P为半圆弧AB上的动点，点Q在斜边BC上，若＝，则的最小值为_______．

Answer 1

【答案】

【解析】

以点为原点，方向为轴正半轴，方向为轴负半轴建立平面直角坐标系，设，利用可求得：，以AB为直径在△ABC外所作半圆的方程为：（），由圆的参数方程可设,,即可整理得：，其中且，再利用正弦函数的性质求得最小为，问题得解。

以点为原点，方向为轴正半轴，方向为轴负半轴建立平面直角坐标系，如下图：

则，,，

所以直线的方程为：，即：，

可设.

所以，,

又，所以，解得：

所以，

以AB为直径在△ABC外所作半圆的方程为：（）

由圆的参数方程可设,,

所以

所以=

，其中且

所以，

当时，最小为