题目内容
|
|=|
|=|
|=1，
+
+
=0，则
•
+
•
+
•
=
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
-
| 3 |
| 2 |
-
．| 3 |
| 2 |
分析：把本题所给的三个向量的和两边平方，得到右边为零，左边是包含要求的三个向量两两求数量积的式子，把已知向量的模代入，得到要求的结果．
解答：解：∵
+
+
=
∴(
+
+
)2=0
∴
2+
2+
2+2（
•
+
•
+
•
）=0
∵|
|=|
|=|
|=1
∴
•
+
•
+
•
=-
故答案为：-
| a |
| b |
| c |
| 0 |
∴(
| a |
| b |
| c |
∴
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| b |
∵|
| a |
| b |
| c |
∴
| a |
| c |
| b |
| c |
| a |
| b |
| 3 |
| 2 |
故答案为：-
| 3 |
| 2 |
点评：本题是一个考查数量积的应用问题，考查学生的计算能力，属于基础题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
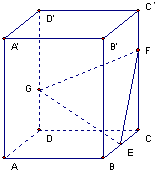如图，正四棱柱ABCD-A′B′C′D′中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为CC′、DD′上的点，且CF=2GD=2．求：