题目内容
(1)数列{an}中,a1=1,an+1=an+2n,求通项公式an.
(2)数列{an}中,a1=4,an+1=
an,求通项公式an?
(2)数列{an}中,a1=4,an+1=
| n+2 | n |
分析:(1)将an+1=an+2n移向得出an+1-an=2n,用累加法求通项公式.
(2)将an+1=
an,变形
=
,用累乘法求通项公式.
(2)将an+1=
| n+2 |
| n |
| an+1 |
| an |
| n+2 |
| n |
解答:解:(1)将an+1=an+2n移向得出an+1-an=2n,
当n≥2时,an=(an-an-1 )+(an-1-an-2 )+…+(a2-a1 )+a1
=2n-1+2n-2+…+2+1
=2n-1,当n=1时,也适合.
∴an=2n-1.
(2)由于an+1=
an,即
=
,
当n≥2时,an=
•
•…•
•
•a1
=
•
•…•
•
•4
=
×4
=2n2+2n,当n=1时,也适合.
∴an=2n2+2n.
当n≥2时,an=(an-an-1 )+(an-1-an-2 )+…+(a2-a1 )+a1
=2n-1+2n-2+…+2+1
=2n-1,当n=1时,也适合.
∴an=2n-1.
(2)由于an+1=
| n+2 |
| n |
| an+1 |
| an |
| n+2 |
| n |
当n≥2时,an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a3 |
| a2 |
| a2 |
| a1 |
=
| n+1 |
| n-1 |
| n |
| n-2 |
| 4 |
| 2 |
| 3 |
| 1 |
=
| (n+1)•n |
| 2 |
=2n2+2n,当n=1时,也适合.
∴an=2n2+2n.
点评:本题考查了数列递推公式,累加法求通项公式.形如an-an-1=f(n)且f(n)能求和,均可以用累加法求通项公式.累乘法求通项公式,形如an-an-1=f(n)an-1且f(n)能求积,均可以用累乘法求通项公式.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
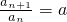 (n∈N*),令bn=an•log2an.
(n∈N*),令bn=an•log2an. (n∈N*),令bn=an•log2an.
(n∈N*),令bn=an•log2an.