题目内容
5．双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{8}$=1的离心率为$\sqrt{3}$．分析 由双曲线解析式得出a与b的值，再利用双曲线的简单性质求出c的值，即可求出离心率e．
解答 解：由双曲线解析式得：a=2，b=2$\sqrt{2}$，
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=2$\sqrt{3}$，
则双曲线的离心率e=$\frac{c}{a}$=$\sqrt{3}$，
故答案为：$\sqrt{3}$．
点评 此题考查了双曲线的简单性质，熟练掌握双曲线的简单性质是解本题的关键．
练习册系列答案
相关题目
13．定义在R上的偶函数f（x）满足：对任意的x1，x2∈（-∞，0]（x1≠x2），有$\frac{{f（{x_2}）-f（{x_1}）}}{{{x_2}-{x_1}}}＜0$，且f（2）=0，则不等式$\frac{2f（x）+f（-x）}{5（x-1）}$＜0的解集是（ ）
| A． | （-∞，-2）∪（2，+∞） | B． | （-∞，-2）∪（1，2） | C． | （-2，1）∪（2，+∞） | D． | （-2，1）∪（1，2） |
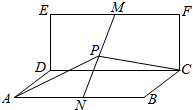如图，矩形CDEF所在的平面与矩形ABCD所在的平面垂直，AD=2$\sqrt{2}$，DE=2，AB=4，点M，N分别为线段EF，AB上的动点，点P为MN的中点，则PA+PC的最小值为2$\sqrt{7}$．