Question

已知函数f(x)=

64

x

与函数g(x)=x

1

3

+t，若f（x）与g（x）的交点在直线y=x的两侧，则实数t的取值范围是（　　）

A．（-6，0]

B．（-6，6）

C．（4，+∞）

D．（-4，4）

Answer 1

分析：题目给出了两个函数f(x)=

64

x

与函数g(x)=x

1

3

+t，首先求出函数y=f（x）与直线y=x的交点A和A^′的坐标（8，8）和（-8，-8），然后做出函数y=g（x）的图象，设其与函数y=f（x）的交点为B和B^′，要保证两个函数图象交点在直线y=x的两侧，则在第一象限B应在A点右侧，在第三象限B^′应在点A^′的左侧，求出三线共点（8，8）和（-8，-8）时t的值，则t的范围可求．

解答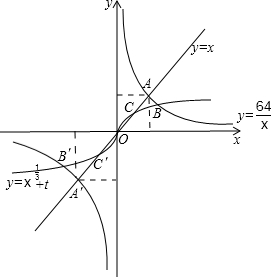：解：设y=x与f（x）的交点为A和A^′，由x=

64

x

得：x=±8，所以A和A^′的坐标分别是（8，8）和（-8，-8），
设f（x）与g（x）的交点为B和B^′，此两动点随着g（x）=x

1

3

+t 图象上下平移而变动，
也就B和B^′位置随t值的变化而在双曲线y=

64

x

上移动．
如图，f（x）与g（x）的交点在直线y=x的两侧，必须B在A的右侧，B^′在A^′的左侧，
设y=x与g（x）的交点为C和C^′，则C和C^′的横坐标要在（-8，8）区间内，
也就是方程x

1

3

+t=x的解在（-8，8）区间内，由图可知：
当t=6时，f（x）=

64

x

，g（x）=x

1

3

+6，y=x，三线共点（8，8）；
当t=-6时，f（x）=

64

x

，g（x）=x

1

3

-6，y=x，三线共点（-8，-8）；
所以t的取值范围是（-6，6）．
故选B．

点评：本题考查了二元一次不等式表示的平面区域，考查了函数的图象，灵活运用数形结合是解答此题的关键，此题是中档题，也是易错题．