题目内容
(1)设{an}是等差数列,且a1-a4-a8-a12+a15=2,求a3+a13及S15的值;(2)等比数列{an}中,a1+an=66,a2an-1=128,前n项的和Sn=126,求n和公比q;
(3)等比数列中q=2,S99=77,求a3+a6+…+a99;
(4)项数为奇数的等差数列{an}中,奇数项之和为80,偶数项之和为75,求此数列的中间项与项数.
思路解析:利用等差或等比数列的性质求解,要多进行整体考虑. 解:(1)由已知,得(a1+a15)-(a4+a12)-a8=2, ∴-a8=2,a8=-2,则a3+a13=2a8=-4, S15= (2)a1an=a2an-1=128,又a1+an=66, ∴ 又Sn= ∴ (3)∵S99=(a1+a4+…+a97)+(a2+a5+…+a98)+(a3+a6+…+a99)=( ∴a3+a6+…a99= (4)设等差数列{an}共有2n-1项, 则 ∴此数列共31项. 中间项为a16,又S奇-S偶=(a1+a3+…+a31)-(a2+a4+…+a30)=a1+(a3-a2)(a5-a4)+…+(a31-a30)=a1+15d=a16=80-75=5. ∴a16=5. 评注:整体思想就是从整体着眼考查所研究的问题中的数列特征、结构特征,以探求解题思想,从而优化简化解题过程的思想方法.在数列中,倘若抓住等差、等比数列的项的性质,整体代值可简化解答过程.![]() =15a8=-30.
=15a8=-30.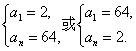
![]() =126,
=126,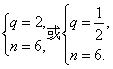
![]() +
+![]() +1)·(a3+a6+…+a99),
+1)·(a3+a6+…+a99),![]() ×77=44.
×77=44.![]() =
=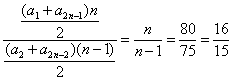
![]() n=16.
n=16.
八斗才期末总动员系列答案
初中生世界系列答案
双休日作业河南人民出版社系列答案
轻负高效优质训练系列答案
双基过关堂堂练系列答案
双基优化训练系列答案
期末预测卷系列答案
初中同步优化测控练习决胜中考系列答案
初中物理实验系列答案
同步练习上海科学技术出版社系列答案
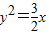 上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.
上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.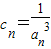 ,求证:
,求证: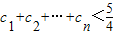 .
.