题目内容
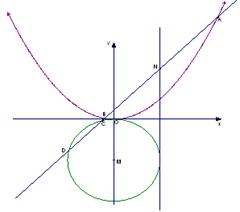
已知抛物线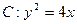 ,直线
,直线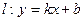 与C交于A,B两点,O为坐标原点。
与C交于A,B两点,O为坐标原点。
(1)当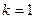 ,且直线
,且直线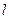 过抛物线C的焦点时,求
过抛物线C的焦点时,求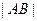 的值;
的值;
(2)当直线OA,OB的倾斜角之和为45°时,求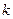 ,
,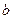 之间满足的关系式,并证明直线
之间满足的关系式,并证明直线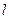 过定点。
过定点。
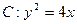 ,直线
,直线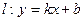 与C交于A,B两点,O为坐标原点。
与C交于A,B两点,O为坐标原点。(1)当
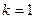 ,且直线
,且直线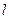 过抛物线C的焦点时,求
过抛物线C的焦点时,求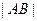 的值;
的值;(2)当直线OA,OB的倾斜角之和为45°时,求
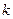 ,
,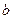 之间满足的关系式,并证明直线
之间满足的关系式,并证明直线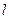 过定点。
过定点。(Ⅰ) 8 (Ⅱ) 直线
直线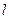 过定点(-4,4)
过定点(-4,4)
 直线
直线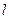 过定点(-4,4)
过定点(-4,4)(1)抛物线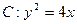 的焦点为(1,0) 2分
的焦点为(1,0) 2分
由已知 =
= ,设
,设 ,
, ,
,
联立 ,消
,消 得
得 ,
,
所以 ,
, 4分
4分



(2)联立 ,消
,消 得
得 ………………(*)(依题意
………………(*)(依题意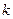 ≠0)
≠0)
 ,
, , 8分
, 8分
设直线OA, OB的倾斜角分别为α,β,斜率分别为 ,
, ,则α+β=45°,
,则α+β=45°,
 ,
, 9分
9分
其中 ,
, ,代入上式整理得
,代入上式整理得 11分
11分
所以 ,即
,即 , 12分
, 12分
此时,使(*)式有解的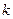 ,
,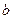 有无数组
有无数组
直线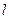 的方程为
的方程为 ,整理得
,整理得
消去 ,即
,即 时
时 恒成立,
恒成立,
所以直线 过定点(-4,4)
过定点(-4,4)
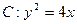 的焦点为(1,0) 2分
的焦点为(1,0) 2分由已知
 =
= ,设
,设 ,
, ,
,联立
 ,消
,消 得
得 ,
,所以
 ,
, 4分
4分


(2)联立
 ,消
,消 得
得 ………………(*)(依题意
………………(*)(依题意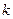 ≠0)
≠0) ,
, , 8分
, 8分设直线OA, OB的倾斜角分别为α,β,斜率分别为
 ,
, ,则α+β=45°,
,则α+β=45°, ,
, 9分
9分其中
 ,
, ,代入上式整理得
,代入上式整理得 11分
11分所以
 ,即
,即 , 12分
, 12分此时,使(*)式有解的
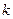 ,
,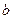 有无数组
有无数组直线
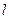 的方程为
的方程为 ,整理得
,整理得
消去
 ,即
,即 时
时 恒成立,
恒成立,所以直线
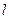 过定点(-4,4)
过定点(-4,4) 
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
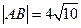 ,求此时抛物线的方程;
,求此时抛物线的方程;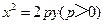 上,其中,点C满足
上,其中,点C满足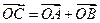 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.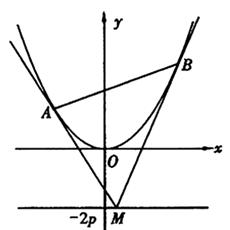
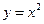 上求一点,使该点到直线
上求一点,使该点到直线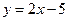 的距离最小,并求最小值.
的距离最小,并求最小值.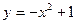
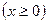 上找一点P
上找一点P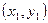 ,其中
,其中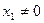 ,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )
,过点P作抛物线的切线,使此切线与抛物线及两坐标轴所围平面图形的面积最小 ( )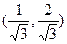
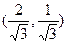
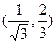
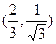
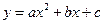 通过点
通过点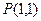 ,且在点
,且在点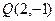 处与直线
处与直线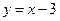 相切,求实数a、b、c的值.
相切,求实数a、b、c的值.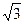 ,若它的一条准线与抛物线y2=4x的准线重合,则该双曲线与抛物线交点到原点的距离是( )
,若它的一条准线与抛物线y2=4x的准线重合,则该双曲线与抛物线交点到原点的距离是( )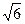
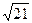
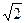
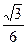 x B.y2=-
x B.y2=-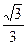 x
x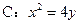 ,圆
,圆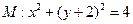 ,
,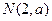 (其中
(其中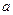 为常数)是
为常数)是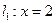 上的点,倾斜角为锐角
上的点,倾斜角为锐角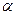 的直线
的直线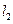 过点
过点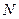 且与抛物线C交于两点A、B,与圆M交于C、D两点.
且与抛物线C交于两点A、B,与圆M交于C、D两点.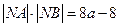 ,且
,且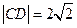 ,求
,求