题目内容
已知函数f(x)= x2-mln
x2-mln +mx(m∈R).
+mx(m∈R).
(1)当m=-1时,求f(x)的单调区间;
(2)当x≥0时,f(x)≥0,求实数m取值范围.
解:(1)当m=-1时,f(x)= x2+ln
x2+ln -x,定义域为(
-x,定义域为( ,+∞),f′(x)=x+
,+∞),f′(x)=x+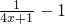 =
=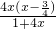 ,
,
当 <x<0或x>
<x<0或x> 时,f′(x)>0;当0<x<
时,f′(x)>0;当0<x< 时,f′(x)<0,
时,f′(x)<0,
∴f(x)的单调增区间为( ,0],[
,0],[ ,+∞),单调减区间为[0,
,+∞),单调减区间为[0, ];(4分)
];(4分)
(2)f(x)= x2-mln
x2-mln +mx,定义域为(
+mx,定义域为( ,+∞),f′(x)=
,+∞),f′(x)=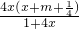 ,(6分)
,(6分)
当m≥ 时,
时,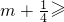 0,当x≥0时,f′(x)≥0,
0,当x≥0时,f′(x)≥0,
∴f(x)在[0,+∞)是增函数,∴当x≥0时,f(x)≥f(0)=0,(8分)
当m< 时,-(m+
时,-(m+ )>0,当0<x<-(m+
)>0,当0<x<-(m+ )时,f′(x)<0,
)时,f′(x)<0,
∴f(x)在[0,-(m+ )]上是减函数,
)]上是减函数,
∴当0≤x≤-(m+ )时,f(x)≤f(0)=0,不适合,(11分)
)时,f(x)≤f(0)=0,不适合,(11分)
∴满足条件的m的取值范围为[ ,+∞).(12分)
,+∞).(12分)
分析:(1)确定函数的定义域为( ,+∞),求导函数,由导数的正负,可得函数的单调区间;
,+∞),求导函数,由导数的正负,可得函数的单调区间;
(2)确定函数的定义域为( ,+∞),求导函数,分类讨论,确定函数的单调性,从而确定m的取值范围.
,+∞),求导函数,分类讨论,确定函数的单调性,从而确定m的取值范围.
点评:本题考查利用导数研究函数的单调性,考查分类讨论思想,属于中档题.
 x2+ln
x2+ln -x,定义域为(
-x,定义域为( ,+∞),f′(x)=x+
,+∞),f′(x)=x+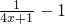 =
=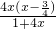 ,
,当
 <x<0或x>
<x<0或x> 时,f′(x)>0;当0<x<
时,f′(x)>0;当0<x< 时,f′(x)<0,
时,f′(x)<0,∴f(x)的单调增区间为(
 ,0],[
,0],[ ,+∞),单调减区间为[0,
,+∞),单调减区间为[0, ];(4分)
];(4分)(2)f(x)=
 x2-mln
x2-mln +mx,定义域为(
+mx,定义域为( ,+∞),f′(x)=
,+∞),f′(x)=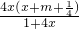 ,(6分)
,(6分)当m≥
 时,
时,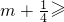 0,当x≥0时,f′(x)≥0,
0,当x≥0时,f′(x)≥0,∴f(x)在[0,+∞)是增函数,∴当x≥0时,f(x)≥f(0)=0,(8分)
当m<
 时,-(m+
时,-(m+ )>0,当0<x<-(m+
)>0,当0<x<-(m+ )时,f′(x)<0,
)时,f′(x)<0,∴f(x)在[0,-(m+
 )]上是减函数,
)]上是减函数,∴当0≤x≤-(m+
 )时,f(x)≤f(0)=0,不适合,(11分)
)时,f(x)≤f(0)=0,不适合,(11分)∴满足条件的m的取值范围为[
 ,+∞).(12分)
,+∞).(12分)分析:(1)确定函数的定义域为(
 ,+∞),求导函数,由导数的正负,可得函数的单调区间;
,+∞),求导函数,由导数的正负,可得函数的单调区间;(2)确定函数的定义域为(
 ,+∞),求导函数,分类讨论,确定函数的单调性,从而确定m的取值范围.
,+∞),求导函数,分类讨论,确定函数的单调性,从而确定m的取值范围.点评:本题考查利用导数研究函数的单调性,考查分类讨论思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|