题目内容
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点, 线段MN经过△ABC的中心G,设Ð MGA=a(
MGA=a( ).
).

(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数;
(2)求y= 的最大值与最小值.
的最大值与最小值.
 MGA=a(
MGA=a( ).
). 
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为a的函数;
(2)求y=
 的最大值与最小值.
的最大值与最小值.解:(1)因为G是边长为1的 正三角形ABC的中心,
正三角形ABC的中心,
所以 AG= ,ÐMAG=
,ÐMAG= ,
,
由正弦定理 .得
.得 .
.
则S1= GM·GA·sina=
GM·GA·sina= .
.
同理可求得S2= .…………………………………6分
.…………………………………6分
(2)y= =
=
=72(3+cot2a).
因为 ,所以当a=
,所以当a= 或a=
或a= 时,y取得最大值 ym a x =240,
时,y取得最大值 ym a x =240,
当a= 时,y取得最小值ymIn=216.…
时,y取得最小值ymIn=216.… ………………
……………… ……………12分
……………12分
 正三角形ABC的中心,
正三角形ABC的中心,所以 AG=
 ,ÐMAG=
,ÐMAG= ,
,由正弦定理
 .得
.得 .
.则S1=
 GM·GA·sina=
GM·GA·sina= .
.同理可求得S2=
 .…………………………………6分
.…………………………………6分(2)y=
 =
=
=72(3+cot2a).
因为
 ,所以当a=
,所以当a= 或a=
或a= 时,y取得最大值 ym a x =240,
时,y取得最大值 ym a x =240,当a=
 时,y取得最小值ymIn=216.…
时,y取得最小值ymIn=216.… ………………
……………… ……………12分
……………12分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
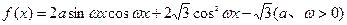 的最大值为2
的最大值为2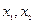 是集合
是集合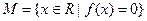 中的任意两个元素,
中的任意两个元素,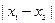 的最小值为
的最小值为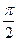 .
.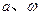 的值
的值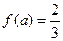 ,求
,求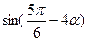 的值
的值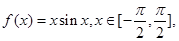
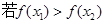 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )



 分14分)已知函数f(x)=2
分14分)已知函数f(x)=2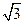 sinxco
sinxco sx-2sin2x.
sx-2sin2x.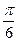 ,
,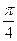 ]上的最大值和最小值.
]上的最大值和最小值. 向量
向量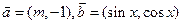 ,
,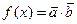 且满足
且满足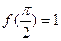 .
.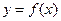 的解析式;
的解析式;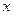 值;
值;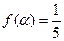 ,求
,求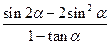 的值.
的值.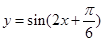 的对称轴可能是 ( )
的对称轴可能是 ( )



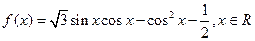 .
.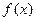 的最小值和最小正周期;
的最小值和最小正周期;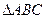 内角
内角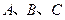 的对边分别为
的对边分别为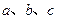 ,且
,且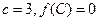 ,若向量
,若向量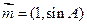 与
与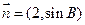 共线,求
共线,求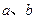 的值.
的值. 在区间
在区间 内的图象是( )
内的图象是( )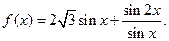
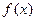 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。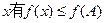 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。