题目内容
设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算积分
f(x)dx,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…xN和y1,y2,…yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分
f(x)dx的近似值为
______.
| ∫ | 10 |
| ∫ | 10 |
由题意可知
≈
得
f(x)dx≈
,
故积分
f(x)dx的近似值为
.
| N1 |
| N |
| ||
| 1 |
| ∫ | 10 |
| N1 |
| N |
故积分
| ∫ | 10 |
| N1 |
| N |

练习册系列答案
相关题目
 ,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…xN和y1,y2,…yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分
,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…xN和y1,y2,…yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分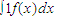 的近似值为 .
的近似值为 .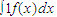 ,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…xN和y1,y2,…yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分
,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…xN和y1,y2,…yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分 的近似值为 .
的近似值为 . ,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…xN和y1,y2,…yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分
,先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…xN和y1,y2,…yN,由此得到N个点(xi,yi)(i=1,2,…,N),再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分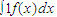 的近似值为 .
的近似值为 .