Question

11．在长方体ABCD-A₁B₁C₁D₁中，其中ABCD是正方形，已知AB=1，AA₁＞1，设点A到直线A₁C的距离和到平面DCB₁A₁的距离分别为d₁，d₂，则$\frac{{d}_{1}}{{d}_{2}}$的取值范围是（$\frac{2\sqrt{3}}{3}$，$\sqrt{2}$）．

Answer 1

分析 设AA₁=b，由AA₁＞1得b＞1，利用长方体中的垂直关系和面积相等求出d₁，连接A₁D、过A作AE⊥A₁D，利用长方体中的垂直关系、线面垂直的判定定理和定义，得到d₂=AE，利用面积相等求出d₂，化简$\frac{{d}_{1}}{{d}_{2}}$，求出$\frac{{d}_{1}}{{d}_{2}}$的范围．

解答 解：设AA₁=b，由AA₁＞1得b＞1，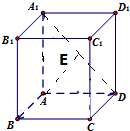
所以点A到直线A₁C的距离d₁=$\frac{A{A}_{1}•AC}{{A}_{1}C}$=$\frac{\sqrt{2}b}{\sqrt{{b}^{2}+2}}$，
连接A₁D，过A作AE⊥A₁D，
由CD⊥平面ADD₁A₁得，CD⊥AE，又AE⊥A₁B，则AE⊥平面DCB₁A₁，
所以AE为点A到平面DCB₁A₁的距离，
则d₂=AE=$\frac{b}{\sqrt{{b}^{2}+1}}$，
所以$\frac{{d}_{1}}{{d}_{2}}$=$\sqrt{2}$•$\frac{\sqrt{{b}^{2}+1}}{\sqrt{{b}^{2}+2}}$=$\sqrt{2}$•$\sqrt{1-\frac{1}{{b}^{2}+2}}$，
因为b＞1，所以b²+2＞3，
所以0＜$\frac{1}{{b}^{2}+2}$＜$\frac{1}{3}$
所以b∈（$\frac{2\sqrt{3}}{3}$，$\sqrt{2}$）．
故答案为：（$\frac{2\sqrt{3}}{3}$，$\sqrt{2}$）．

点评 本题的考点是点、线、面间的距离计算，线面垂直的判定定理和定义，面积相等法求距离，关键是利用长方体的几何特征寻找表示点面距离的线段，属于中档题．