题目内容
已知函数
=|x+1|-2|x-a|，a>0.
（Ⅰ）当a=1时，求不等式
f(x)>1的解集；
（Ⅱ）若f(x)的图像与x轴围成的三角形面积大于6，求a的取值范围
新课标快乐提优暑假作业陕西旅游出版社系列答案
，乙队中3人答对的概率分别为
，
，且各人回答正确与否相互之间没有影响，用
表示乙队的总得分．某中学点差了某班全部45名同学参加书法社团和演讲社团的情况，数据如下表：（单位：人）
| 参加书法社团 | 未参加书法社团 | |
| 参加演讲社团 | 8 | 5 |
| 未参加演讲社团 | 2 | 30 |
（1） 从该班随机选1名同学，求该同学至少参加上述一个社团的概率；
（2） 在既参加书法社团又参加演讲社团的8名同学中，有5名男同学A1，A2，A3，A4，A5,3名女同学B1，B2，B3.现从这5名男同学和3名女同学中各随机选1人，求A1被选中且B1未被选中的概率。
1，若存在唯一的整数x0，使得f（x0）
，1） B. [-
） C. [某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费x1和年销售量y1（i=1,2，···，8）数据作了初步处理，得到下面的散点图及一些统计量的值。
|
|
|
|
|
|
|
|
| 46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
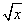（x1-表中w1 =
1, ，
=
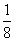
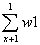
（1） 根据散点图判断，y=a+bx与y=c+d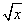哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）以知这种产品的年利率z与x、y的关系为z=0.2y-x。根据（Ⅱ）的结果回答下列问题：
（i） 年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii） 年宣传费x为何值时，年利率的预报值最大？
附：对于一组数据（u1 v1）,（u2 v2）…….. （un vn）,其回归线v=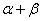
u的斜率和截距的最小二乘估计分别为：
的导函数，f（-1）=0，当x>0时，
，则使得f (x) >0成立的x的取值范围是
（B）
（D）
B．
C．
D．5