题目内容
已知函数 ,若对任意x∈[3,+∞),f(x)>0恒成立,则实数a的取值范围
,若对任意x∈[3,+∞),f(x)>0恒成立,则实数a的取值范围
- A.

- B.

- C.(-∞,4)
- D.

B
分析:此题要学会转化,对任意x∈[3,+∞),f(x)>0恒成立,转化为x2-ax+a>0恒成立,然后再分离常数a,进行求解;
解答:∵函数 ,若对任意x∈[3,+∞),f(x)>0恒成立,
,若对任意x∈[3,+∞),f(x)>0恒成立,
∴x2-ax+a>0,对任意x∈[3,+∞),恒成立,
分离常数得,a<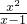 ,求出
,求出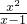 的最小值即可,
的最小值即可,
∵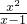 =
= +(x-1)+2,令x-1=t,得f(t)=
+(x-1)+2,令x-1=t,得f(t)= +t+2(t≥2),
+t+2(t≥2),
函数f(t)在[2,+∞)上为增函数,fmin(t)=f(2)= ,
,
∴a< ,
,
故选B.
点评:此题考查函数的恒成立问题,利用了常数分离法,这是一种比较简便的方法;
分析:此题要学会转化,对任意x∈[3,+∞),f(x)>0恒成立,转化为x2-ax+a>0恒成立,然后再分离常数a,进行求解;
解答:∵函数
 ,若对任意x∈[3,+∞),f(x)>0恒成立,
,若对任意x∈[3,+∞),f(x)>0恒成立,∴x2-ax+a>0,对任意x∈[3,+∞),恒成立,
分离常数得,a<
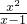 ,求出
,求出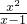 的最小值即可,
的最小值即可,∵
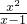 =
= +(x-1)+2,令x-1=t,得f(t)=
+(x-1)+2,令x-1=t,得f(t)= +t+2(t≥2),
+t+2(t≥2),函数f(t)在[2,+∞)上为增函数,fmin(t)=f(2)=
 ,
,∴a<
 ,
,故选B.
点评:此题考查函数的恒成立问题,利用了常数分离法,这是一种比较简便的方法;

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ,若对任意x∈R,都有
,若对任意x∈R,都有 ,则
,则 =____.
=____. ,若对任意x∈R,都有
,若对任意x∈R,都有 ,则
,则 =
.
=
. ,若对任意x∈(0,1)恒有f(x)>1,求a的取值范围.
,若对任意x∈(0,1)恒有f(x)>1,求a的取值范围. ,若对任意x∈[1,+∞),f(x)>0恒成立,求实数m的取值范围.
,若对任意x∈[1,+∞),f(x)>0恒成立,求实数m的取值范围. ,若对任意x∈(0,+∞)都有f(x)≤g(x)成立,则实数a的取值范围是 .
,若对任意x∈(0,+∞)都有f(x)≤g(x)成立,则实数a的取值范围是 .