题目内容
【题目】△ABC中,角A,B,C所对边分别为a,b,c,a=2,B=45°,①当b= ![]() 时,三角形有个解;②若三角形有两解,则b的取值范围是 .
时,三角形有个解;②若三角形有两解,则b的取值范围是 .
【答案】1;(2,2 ![]() )
)
【解析】解:①∵△ABC中,角A,B,C所对边分别为a,b,c, a=2,B=45°,b= ![]() ,
,
由正弦定理 ![]() ,得
,得 ![]() ,
,
解得sinA=1,∴A=90°,三角形只有一个解.
所以答案是:1.
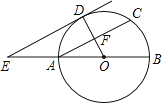
②BC=a=2,要使三角形有两解,就是要使以C为圆心,半径为2的圆与BA有两个交点,
当A=90°时,圆与AB相切;
当A=45°时交于B点,也就是只有一解,
∴45°<A<90°,即 ![]() <sinA<1,
<sinA<1,
由正弦定理以及asinB=bsinA.可得:b=x= ![]() =2
=2 ![]() sinA,
sinA,
∵2 ![]() sinA∈(2,2
sinA∈(2,2 ![]() ).
).
∴b的取值范围是(2,2 ![]() ).
).
所以答案是:(2,2 ![]() ).
).
【考点精析】认真审题,首先需要了解正弦定理的定义(正弦定理:![]() ).
).

练习册系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合计 |
| 1 |

(1)求出表中![]() 及图中
及图中![]() 的值;
的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间![]() 内的概率.
内的概率.