题目内容
17.已知x,y∈R*,2y+x-xy=0,若x+2y>m2+2m恒成立,则m的取值范围是(-4,2).分析 方程成立为2y+x=xy,同时除以xy得$\frac{2}{x}+\frac{1}{y}$=1,利用均值定理的变形可得$\frac{2}{x}$•$\frac{1}{y}$≤$(\frac{\frac{2}{x}+\frac{1}{y}}{2})^{2}$=$\frac{1}{4}$,得出xy≥8(当x=2y时,等号成立),再次利用均值定理求出x+2y的最小值,进而得出m的范围.
解答 解:2y+x-xy=0,
∴2y+x=xy,
∴$\frac{2}{x}+\frac{1}{y}$=1,
∵$\frac{2}{x}$•$\frac{1}{y}$≤$(\frac{\frac{2}{x}+\frac{1}{y}}{2})^{2}$=$\frac{1}{4}$,
∴xy≥8(当x=2y时,等号成立),
∵x+2y≥2$\sqrt{2xy}$≥8(当x=2y时,等号成立),
∴m2+2m<8,解得-4<m<2.
故答案为为(-4,2).
点评 考查了均值定理的应用和恒成立问题的转换.应注意均值定理中等号成立的条件.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
7.已知全集为R,集合A={x|($\frac{1}{2}$)x≤1},B={x|x≥2},A∩(∁RB)=( )
| A. | [0,2) | B. | [0,2] | C. | (1,2) | D. | (1,2] |
12.(理)现有11个保送大学的名额分配给8个班级,每班至少有1个名额,则名额分配的方法共有( )
| A. | 56种 | B. | 112种 | C. | 120种 | D. | 240种 |
6.已知a>0,b>0,且a+b=ab,则a+$\frac{b}{4}$的最小值为( )
| A. | 1 | B. | $\frac{7}{4}$ | C. | 2 | D. | $\frac{9}{4}$ |
7.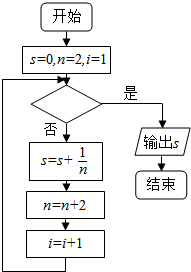 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个流程图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个流程图,其中判断框内应填入的条件是( )
 如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个流程图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个流程图,其中判断框内应填入的条件是( )| A. | i≤21 | B. | i≤11 | C. | i≥21 | D. | i≥11 |