��Ŀ����
1����֪��Բ����$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������ԭ�������ֱ��l1��l2�ֱ��릣���ڵ�A��B��C��D���õ�ƽ���ı���ACBD����1����ACBDΪ������ʱ����������ε����S��
��2����ֱ��l1��l2����y��Գƣ���������һ��P��l1��l2�ľ���ֱ�Ϊd1��d2����d12+d22Ϊ��ֵʱ�����ʱֱ��l1��l2��б�ʼ��ö�ֵ��
��3����ACBDΪ���Σ���Բx2+y2=1����������ACBDʱ����a��b����Ĺ�ϵʽ��
���� ��1��ͨ��ACBDΪ�����ο�ֱ֪��l1��l2�ķ���Ϊy=x��y=-x����������ֱ������Բ���̣����öԳ��Լ��ý��ۣ�
��2��ͨ������ֱ��l1�ķ���Ϊy=kx����ֱ��l2�ķ���Ϊy=-kx����P��x0��y0�������õ㵽ֱ�ߵľ��빫ʽ��$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1��������֪${{d}_{1}}^{2}$+${{d}_{2}}^{2}$�ı���ʽ����������d12+d22Ϊ��ֵ���㼴�ý��ۣ�
��3��ͨ����AC��Բx2+y2=1���е��е�����Ϊ��x0��y0������������AC�ķ�������Բ���̣���x0=0��y0=0��x0��0��y0��0����������ۼ��ɣ�
��� �⣺��1����ACBDΪ�����Σ�
��ֱ��l1��l2�ķ���Ϊy=x��y=-x��
���A��B��������x1��y1������x2��y2����
�ⷽ����$\left\{\begin{array}{l}{y=x}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$����${{x}_{1}}^{2}$=${{x}_{2}}^{2}$=$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$��
�ɶԳ��Կ�֪��S=4${{x}_{1}}^{2}$=$\frac{4{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$��
��2�������⣬������ֱ��l1�ķ���Ϊy=kx����ֱ��l2�ķ���Ϊy=-kx��
��P��x0��y0������$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1��
�֡�d1=$\frac{|k{x}_{0}-{y}_{0}|}{\sqrt{1+{k}^{2}}}$��d2=$\frac{|k{x}_{0}+{y}_{0}|}{\sqrt{1+{k}^{2}}}$��
��${{d}_{1}}^{2}$+${{d}_{2}}^{2}$=$\frac{��k{x}_{0}-{y}_{0}��^{2}}{1+{k}^{2}}$+$\frac{��k{x}_{0}+{y}_{0}��^{2}}{1+{k}^{2}}$=$\frac{2{k}^{2}{{x}_{0}}^{2}+2{{y}_{0}}^{2}}{1+{k}^{2}}$��
��${{y}_{0}}^{2}$=b2��1-$\frac{{{x}_{0}}^{2}}{{a}^{2}}$��������ʽ��
��${{d}_{1}}^{2}$+${{d}_{2}}^{2}$=$\frac{2��{k}^{2}-\frac{{b}^{2}}{{a}^{2}}��{{x}_{0}}^{2}+2{b}^{2}}{1+{k}^{2}}$��
��d12+d22Ϊ��ֵ��
��k2-$\frac{{b}^{2}}{{a}^{2}}$=0����k=��$\frac{b}{a}$��
����ֱ��l1��l2��б�ʷֱ�Ϊ$\frac{b}{a}$��-$\frac{b}{a}$����ʱ${{d}_{1}}^{2}$+${{d}_{2}}^{2}$=$\frac{2{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$��
��3����AC��Բx2+y2=1���е��е�����Ϊ��x0��y0����
������AC�ķ���Ϊ��x0x+y0y=1��
��A��C������Ϊ��x1��y1������x2��y2��Ϊ������$\left\{\begin{array}{l}{{x}_{0}x+{y}_{0}y=1}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$��ʵ���⣮
�ٵ�x0=0��y0=0ʱ��ACBD��Ϊ�����Σ�
��Բ�����㣨1��1����������$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1��
�ڵ�x0��0��y0��0ʱ����y=$\frac{1}{{y}_{0}}$��1-x0x������$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��
�������a2${{x}_{0}}^{2}$+b2${{y}_{0}}^{2}$��x2-2a2x0x-a2��1+b2${{y}_{0}}^{2}$��=0��
��Τ�ﶨ����֪x1x2=$\frac{{a}^{2}��1-{b}^{2}{{y}_{0}}^{2}��}{{a}^{2}{{x}_{0}}^{2}+{b}^{2}{{y}_{0}}^{2}}$��
ͬ����֪y1y2=$\frac{{b}^{2}��1-{a}^{2}{{x}_{0}}^{2}��}{{a}^{2}{{x}_{0}}^{2}+{b}^{2}{{y}_{0}}^{2}}$��
��ACBD����
��AO��CO����x1x2+y1y2=0��
��$\frac{{a}^{2}��1-{b}^{2}{{y}_{0}}^{2}��}{{a}^{2}{{x}_{0}}^{2}+{b}^{2}{{y}_{0}}^{2}}$+$\frac{{b}^{2}��1-{a}^{2}{{x}_{0}}^{2}��}{{a}^{2}{{x}_{0}}^{2}+{b}^{2}{{y}_{0}}^{2}}$=0��
�����ã�a2+b2=a2b2��${{x}_{0}}^{2}$+${{y}_{0}}^{2}$����
�֡�${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=1��
��a2+b2=a2b2����$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1��
����������a��b����Ĺ�ϵʽΪ$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1��
���� ������һ��ֱ����Բ���ߵ��ۺ��⣬����������۵�˼�룬�����������������ע����ⷽ���Ļ��ۣ������е��⣮

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�ijͬѧ�����ڼ����30λ��������ʳϰ�߽�����һ�ε��飬�г������� ��������
��������
ƫ���߲� | ƫ������ | �ϼ� | |
50������ | 4 | 8 | 12 |
50������ | 16 | 2 | 18 |
�ϼ� | 20 | 10 | 30 |
�����˵����������ʳϰ���������йصİ���Ϊ�� ��
A��90% B��95% C��99% D��99.9%
�����ο���ʽ���ٽ�ֵ��
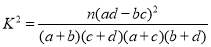
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
| A�� | [-2��2] | B�� | ��-�ޣ�-2]��[2��+�ޣ� | C�� | [-$\frac{1}{2}$��$\frac{1}{2}$] | D�� | ��-�ޣ�-$\frac{1}{2}$]��[$\frac{1}{2}$��+�ޣ� |


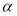 �ձ��뵥λԲ
�ձ��뵥λԲ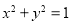 �Ľ���Ϊ
�Ľ���Ϊ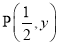 ����
����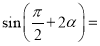 �� ��
�� �� B��
B��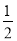 C��
C��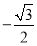 D��
D��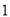
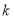 ��ֱ��
��ֱ�� ��Բ
��Բ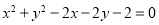 ��λ�ù�ϵ��________
��λ�ù�ϵ��________ B.
B.  C.
C. 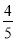 D.
D. 