题目内容
已知13sinα+5cosβ=9,13cosα+5sinβ=15,那么sin(α+β)的值为 .
【答案】分析:将已知条件中的两个等式平方相加,利用三角函数的平方关系及两角和的正弦公式求出sin(α+β)的值
解答:解:∵13sinα+5cosβ=9,13cosα+5sinβ=15
两式平方相加得
194+130sinαcosβ+130cosαsinβ=306
即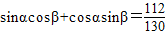
∴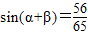
故答案为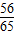
点评:解决三角函数中的给值求值题,一般通过观察,从整体上处理;一般利用三角函数的诱导公式、倍角公式、两角和、差公式.
解答:解:∵13sinα+5cosβ=9,13cosα+5sinβ=15
两式平方相加得
194+130sinαcosβ+130cosαsinβ=306
即
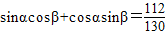
∴
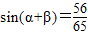
故答案为
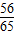
点评:解决三角函数中的给值求值题,一般通过观察,从整体上处理;一般利用三角函数的诱导公式、倍角公式、两角和、差公式.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目