题目内容
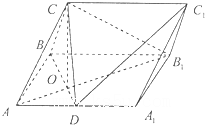 在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=
在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=| 2 |
(Ⅰ)证明:BC⊥AB1;
(Ⅱ)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
分析:(Ⅰ)要证明BC⊥AB1,可证明AB1垂直于BC所在的平面BCD,已知CO垂直于侧面ABB1A1,所以CO垂直于AB1,只要在矩形ABB1A1内证明BD垂直于AB1即可,可利用角的关系加以证明;
(Ⅱ)分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,求出
,平面ABC的一个法向量,利用向量的夹角公式,即可得出结论.
(Ⅱ)分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,求出
| DC1 |
解答: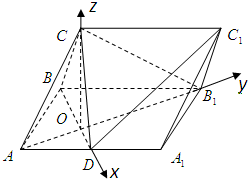 (I)证明:由题意,因为ABB1A1是矩形,
(I)证明:由题意,因为ABB1A1是矩形,
D为AA1中点,AB=1,AA1=
,AD=
,
所以在直角三角形ABB1中,tan∠AB1B=
,
在直角三角形ABD中,tan∠ABD=
,
所以∠AB1B=∠ABD,
又∠BAB1+∠AB1B=90°,∠BAB1+∠ABD=90°,
所以在直角三角形ABO中,故∠BOA=90°,
即BD⊥AB1,
又因为CO⊥侧面ABB1A1,AB1?侧面ABB1A1,
所以CO⊥AB1
所以,AB1⊥面BCD,
因为BC?面BCD,
所以BC⊥AB1.
(Ⅱ)解:如图,分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,则A(0,-
,0),B(-
,0,0),C(0,0,
),B1(0,
,0),D(
,0,0),
又因为
=2
,所以C1(
,
,
)
所以
=(-
,
,0),
=(0,
,
),
=(
,
,
),
设平面ABC的法向量为
=(x,y,z),
则根据
可得
=(1,
,-
)是平面ABC的一个法向量,
设直线C1D与平面ABC所成角为α,则sinα=
=
.
 (I)证明:由题意,因为ABB1A1是矩形,
(I)证明:由题意,因为ABB1A1是矩形,D为AA1中点,AB=1,AA1=
| 2 |
| ||
| 2 |
所以在直角三角形ABB1中,tan∠AB1B=
| AB |
| BB1 |
在直角三角形ABD中,tan∠ABD=
| AD |
| AB1 |
所以∠AB1B=∠ABD,
又∠BAB1+∠AB1B=90°,∠BAB1+∠ABD=90°,
所以在直角三角形ABO中,故∠BOA=90°,
即BD⊥AB1,
又因为CO⊥侧面ABB1A1,AB1?侧面ABB1A1,
所以CO⊥AB1
所以,AB1⊥面BCD,
因为BC?面BCD,
所以BC⊥AB1.
(Ⅱ)解:如图,分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,则A(0,-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 6 |
又因为
| CC1 |
| AD |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
所以
| AB |
| ||
| 3 |
| ||
| 3 |
| AC |
| ||
| 3 |
| ||
| 3 |
| DC1 |
| ||
| 6 |
2
| ||
| 3 |
| ||
| 3 |
设平面ABC的法向量为
| n |
则根据
|
| n |
| 2 |
| 2 |
设直线C1D与平面ABC所成角为α,则sinα=
|
| ||||
|
|
3
| ||
| 55 |
点评:本题考查了直线与平面垂直的性质,考查线面角,考查向量方法的运用,属于中档题.

练习册系列答案
相关题目
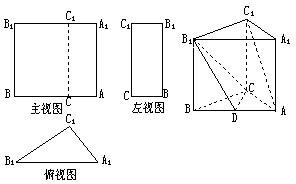 已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,
已知三棱柱ABC-A1B1C1的三视图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5, 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
(2012•江西)在三棱柱ABC-A1B1C1中,已知AB=AC=AA1= (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.