题目内容
已知二次函数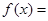
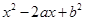 (
(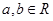 ),若
),若 是从区间
是从区间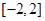 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间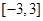 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程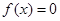 没有实数根的概率.
没有实数根的概率.
方程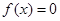 没有实数根的概率为
没有实数根的概率为 .
.
解析试题分析:先由二次方程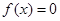 没有实数根得到
没有实数根得到 即
即 ,然后结合
,然后结合 的取值范围作出不等式
的取值范围作出不等式 与
与 的平面区域,最后由几何概型的概率计算公式可得所要求的概率.
的平面区域,最后由几何概型的概率计算公式可得所要求的概率.
试题解析:由方程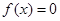 没有实数根,得:
没有实数根,得: 即
即 或者
或者 ,又因为
,又因为
作出平面区域图如下图所示 8分
可知方程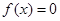 没有实数根的概率为:
没有实数根的概率为:
故方程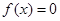 没有实数根的概率为
没有实数根的概率为 12分.
12分.
考点:1.几何概型的概率问题;2.二次方程的根的个数与判别式的关系;3.数形结合的思想.

练习册系列答案
相关题目
某公司研制出一种新型药品,为测试该药品的有效性,公司选定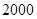 个药品样本分成三组,测试结果如下表:
个药品样本分成三组,测试结果如下表:
| 分组 | 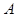 组 组 | 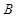 组 组 |  组 组 |
| 药品有效 | 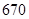 | 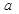 | 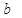 |
| 药品无效 | 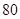 | 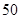 | 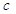 |
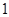 个,抽到
个,抽到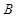 组药品有效的概率是
组药品有效的概率是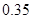 .
.(1)现用分层抽样的方法在全体样本中抽取
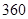 个测试结果,问应在
个测试结果,问应在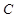 组抽取样本多少个? [来源:学优]
组抽取样本多少个? [来源:学优](2)已知
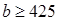 ,
,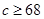 ,求该药品通过测试的概率(说明:若药品有效的概率不小于
,求该药品通过测试的概率(说明:若药品有效的概率不小于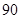 %,则认为测试通过).
%,则认为测试通过). 在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
(2)若这2人来自区域A,D,并记来自区域A队员中的人数为X,求随机变量X的分布列及数学期望.
 年
年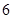 月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为
月“神舟 ”发射成功.这次发射过程共有四个值得关注的环节,即发射、实验、授课、返回.据统计,由于时间关系,某班每位同学收看这四个环节的直播的概率分别为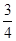 、
、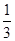 、
、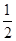 、
、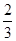 ,并且各个环节的直播收看互不影响.
,并且各个环节的直播收看互不影响. 名同学至少有
名同学至少有 名同学收看发射直播的概率;
名同学收看发射直播的概率;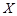 表示该班某一位同学收看的环节数,求
表示该班某一位同学收看的环节数,求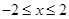 ,
,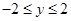 ,点
,点 的坐标为
的坐标为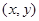 .
.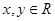 时,点
时,点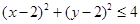 的概率;
的概率;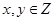 时,点
时,点 表示.
表示.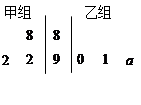
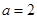 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为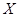 ,求随机变量
,求随机变量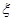 为取出的3枝里一等品的枝数,求
为取出的3枝里一等品的枝数,求 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;汽车走公路②堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.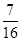 ,求走公路②堵车的概率;
,求走公路②堵车的概率;