题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数 ![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)求证:  (
(![]() ,
, ![]() 是自然对数的底数).
是自然对数的底数).
【答案】(Ⅰ)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅱ)
;(Ⅱ)![]() ; (Ⅲ)见解析.
; (Ⅲ)见解析.
【解析】分析:(Ⅰ)求出函数的导数,分别解不等式![]() 、
、![]() ,可求得
,可求得![]() 的增区间和减区间.
的增区间和减区间.
(Ⅱ)构建新函数![]() , 不等式
, 不等式![]() 在
在![]() 上恒成立等价于
上恒成立等价于![]() 在
在![]() 恒成立,而
恒成立,而![]() ,分
,分![]() 三种情形讨论可得实数
三种情形讨论可得实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅲ)由(Ⅱ)得不等式![]() ,
, ![]() ,故有
,故有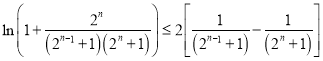 ,利用累加及其裂项相消法可以得到:
,利用累加及其裂项相消法可以得到: 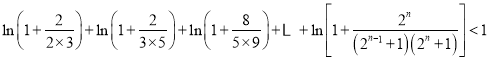 ,化简后可得到要证明的不等式.
,化简后可得到要证明的不等式.
详解:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]() .
.
由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() ,
,
故函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)因当![]() 时,不等式
时,不等式![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
设![]() ,只需
,只需![]() 即可.
即可.
由![]() ,
,
(ⅰ)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
故![]() 成立;
成立;
(ⅱ)当![]() 时,由
时,由![]() ,因
,因![]() ,所以
,所以![]() ,
,
①若![]() ,即
,即![]() 时,在区间
时,在区间![]() 上,
上, ![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() 在
在![]() 上无最大值;
上无最大值;
②若![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,同样
上单调递增,同样![]() 在
在![]() 上无最大值,不满足条件;
上无最大值,不满足条件;
(ⅲ)当![]() 时,由
时,由![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,故函数
,故函数![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 成立.
成立.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)据(Ⅱ)知当![]() 时,
时, ![]() 在
在![]() 上恒成立,又
上恒成立,又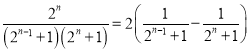 ,
,
∵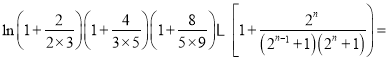
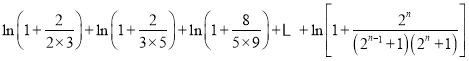
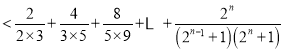
![]() ,
,
∴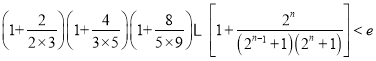 .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目