题目内容

函数f（x）是由向量集
A
到
A
的映射f确定，且f（x）=x-2（x•
a
）
a
，若存在非零常向量
a
使f[f（x）]=f（x）恒成立．
（1）求|
a
|；
（2）设
AB
=
a
，
A
（1，-2），若点P分
AB
的比为-
1
3
，求点P所在曲线的方程．
（1）f[f （x）]=f （x）-2[f （x）•
a
]•
a
（
x
为向量）
=x-2（x•
a
）•
a
-2{[x-2（x•
a
）•
a
]•
a
}•
a

=x-2（x•
a
）•
a
-2[x•
a
-2（x•
a
）
a
2]•
a
=x-2（x•
a
）•
a

∴[x•
a
-2（x•
a
）•
a
2]•
a
=0，∵
a
≠
0
．
∴x•
a
-2（x•
a
）•
a
2=0，∴x•
a
（1-2
a
2）=0恒成立
∴1-2
a
2=0，∴
a
2=
1
2
，∴|
a
|=
2
2
．
（2）设B（x′，y′），∴
AB
=（x′-1，y′+2），
∴（x′-1）2+（y′+2）2=
1
2
，
设P（x，y） 由
AP
=-
1
3
PB
，∴（x-1，y+2）=-
1
3
（x′-x，y′-y）
∴
x-1=-
1
3
(x′-x)
y+2=-
1
3
(y′-y)
，解得
x′=-2x+3
y′=-2y-6
，
∴（-2x+3-1）2+（-2y-6+2）2=
1
2

∴（x-1）2+（y+2）2=
1
8
，即为P点所在曲线的方程．
练习册系列答案
相关题目
将函数f（x）的图象上所有点的横坐标伸长到原来的2倍，同时将纵坐标缩小到原来的
1
2
倍，得到函数y=cos（x-
π
6
）的图象，另一方面函数f（x）的图象也可以由函数y=2cos2x+1的图象按向量
c
平移得到，则
c
可以是（　　）
A、(
π
6
，-1)
B、(
π
12
，1)
C、(
π
12
，-1)
D、(
π
6
，1)
函数f（x）是由向量集
A
到
A
的映射f确定，且f（x）=x-2（x•
a
）
a
，若存在非零常向量
a
使f[f（x）]=f（x）恒成立．
（1）求|
a
|；
（2）设
AB
=
a
，
A
（1，-2），若点P分
AB
的比为-
1
3
，求点P所在曲线的方程．
（2010•合肥模拟）已知向量
a
=(sinx，cosx)，
b
=(cosx，
3
cosx)，f(x)=
a
•
b
-
3
2
，下面关于函数f（x）的导函数f'（x）说法中错误的是（　　）
函数f（x）是由向量集到的映射f确定，且f（x）=x-2，若存在非零常向量使f[f（x）]=f（x）恒成立．
（1）求||；
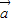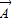（2）设=，（1，-2），若点P分的比为-，求点P所在曲线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网