题目内容
四个函数y=x-1,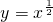 ,y=x2,y=x3,y=lnx,
,y=x2,y=x3,y=lnx, 中,在区间(0,+∞)上为减函数的是________.
中,在区间(0,+∞)上为减函数的是________.
y=x-1, .
.
分析:根据幂函数、指数函数、对数函数的性质逐项判断即可找出符合条件的答案.
解答:对幂函数y=xa,当a<0时在(0,+∞)上为减函数,a>0时在(0,+∞)上为增函数
所以y=x-1在(0,+∞)上为减函数,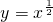 ,y=x2,y=x3在(0,+∞)上为增函数;
,y=x2,y=x3在(0,+∞)上为增函数;
对指数函数y=ax(a>0,且a≠1),当a>1时在R上为增函数,当0<a<1时在R上为减函数,
所以 在(0,+∞)上为减函数,
在(0,+∞)上为减函数,
对对数函数y=logax(a>0,且a≠1),当a>1时在(0,+∞)上为增函数,当0<a<1时在(0,+∞)上为减函数,
所以y=lnx(0,+∞)上为增函数,
故答案为:y=x-1, .
.
点评:本题考查幂函数、指数函数、对数函数的单调性,属基础题.
 .
.分析:根据幂函数、指数函数、对数函数的性质逐项判断即可找出符合条件的答案.
解答:对幂函数y=xa,当a<0时在(0,+∞)上为减函数,a>0时在(0,+∞)上为增函数
所以y=x-1在(0,+∞)上为减函数,
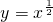 ,y=x2,y=x3在(0,+∞)上为增函数;
,y=x2,y=x3在(0,+∞)上为增函数;对指数函数y=ax(a>0,且a≠1),当a>1时在R上为增函数,当0<a<1时在R上为减函数,
所以
 在(0,+∞)上为减函数,
在(0,+∞)上为减函数,对对数函数y=logax(a>0,且a≠1),当a>1时在(0,+∞)上为增函数,当0<a<1时在(0,+∞)上为减函数,
所以y=lnx(0,+∞)上为增函数,
故答案为:y=x-1,
 .
.点评:本题考查幂函数、指数函数、对数函数的单调性,属基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目