题目内容
20.设集合M={(m,n)|0<m<2,0<n<2,m,n∈R},则任取(m,n)∈M,关于x的方程mx2+2x+n=0有实根的概率为( )| A. | $\frac{1+ln2}{2}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1-ln2}{2}$ | D. | $\frac{3-2ln2}{4}$ |
分析 首先根据关于x的方程mx2+2x+n=0有实根,推得ac≤1;然后作出图象,求出相应的面积;最后根据几何概型的概率的求法,关于x的方程mx2+2x+n=0有实根的概率即可.
解答  解:若关于x的方程mx2+2x+n=0有实根,则△=22-4mn≥0,
解:若关于x的方程mx2+2x+n=0有实根,则△=22-4mn≥0,
∴mn≤1;
∵M={(m,n)|0<m<2,0<n<2,m,n∈R},总事件表示的面积为2×2=4,
方程有实根时,表示的面积为2×$\frac{1}{2}$+2×${∫}_{\frac{1}{2}}^{1}$$\frac{1}{m}$dm=1+lnm|${\;}_{\frac{1}{2}}^{1}$=1+2ln2,
∴关于x的方程mx2+2x+n=0有实根的概率为$\frac{1+2ln2}{4}$,
故选:B.
点评 本题主要考查了几何概型的应用,考查了二元一次方程的根的判断,考查了数形结合的思想,属于中档题.

练习册系列答案
相关题目
11.复数$\frac{1}{1+i}$的虚部是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
8.某市家庭煤气的使用量x(m3)和煤气费f(x)(元)满足关系f(x)=$\left\{\begin{array}{l}{C,0<x≤A}\\{C+B(x-A),x>A}\end{array}\right.$,已知某家庭今年前三个月的煤气费如表
若四月份该家庭使用了20m3的煤气,则其煤气费为( )
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
| A. | 11.5元 | B. | 11元 | C. | 10.5元 | D. | 10元 |
15.已知向量$\overrightarrow{a}$=(-2,1),与$\overrightarrow{b}$=(m,3)平行,则m=( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
12.某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在[50,100]内,发布成绩使用等级制.各等级划分标准见表.规定:A、B、C三级为合格等级,D为不合格等级.
为了解该校高一年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
(I)求n和频率分布直方图中的x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中,从A、C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示所抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.
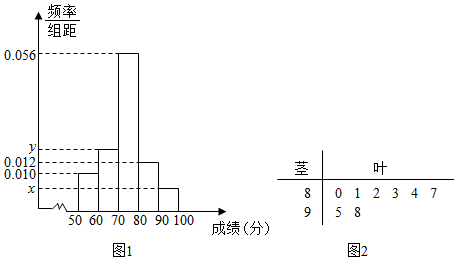
| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
(I)求n和频率分布直方图中的x,y的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生中任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中,从A、C两个等级的学生中随机抽取了3名学生进行调研,记ξ表示所抽取的3名学生中为C等级的学生人数,求随机变量ξ的分布列及数学期望.
