题目内容
函数f（x）=sinx+x-1的图象不经过的象限是（ ）
分析：先求导f′（x）=cosx+1≥0，得出函数f（x）=sinx+x-1在R上是单调增函数，且f（x）=sinx+x-1的零点在原点的右侧，从而得出函数f（x）=sinx+x-1的图象不经过第二象限．
解答：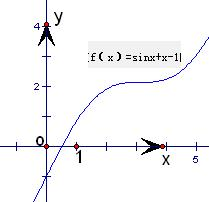
解：∵f（x）=sinx+x-1
∴f′（x）=cosx+1≥0，∴函数f（x）=sinx+x-1在R上是单调增函数，
且f（x）=sinx+x-1的零点在原点的右侧，如图．
∴函数f（x）=sinx+x-1的图象不经过第二象限．
故选B．
解：∵f（x）=sinx+x-1∴f′（x）=cosx+1≥0，∴函数f（x）=sinx+x-1在R上是单调增函数，
且f（x）=sinx+x-1的零点在原点的右侧，如图．
∴函数f（x）=sinx+x-1的图象不经过第二象限．
故选B．
点评：本小题主要考查函数单调性的应用、正弦函数的图象、函数的图象等基础知识，考查运算求解能力，考查数形结合思想，属于基础题．
练习册系列答案
相关题目
函数f（x）=sin（ωx+?）（x∈R，ω＞0，0≤?＜2π）的部分图象如图，则