题目内容
若函数f(x)在R+上是单调递增函数,f-1(a+1)<f-1(a2-1),试求a的范围.
解:f-1(a+1)<f-1(a2-1)
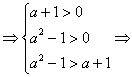 a>2.
a>2.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
题目内容
若函数f(x)在R+上是单调递增函数,f-1(a+1)<f-1(a2-1),试求a的范围.
解:f-1(a+1)<f-1(a2-1)
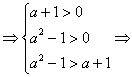 a>2.
a>2.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案