题目内容
已知椭圆C的中心在坐标原点，焦点在x轴上且过点P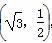
，离心率是
.
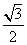(1)求椭圆C的标准方程；
(2)直线l过点E (－1,0)且与椭圆C交于A，B两点，若|EA|＝2|EB|，求直线l的方程．
解析： (1)设椭圆C的标准方程为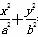
＝1(a＞b＞0)．
由已知可得
，
解得a2＝4，b2＝1.
故椭圆C的标准方程为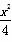
＋y2＝1.
(2)由已知，若直线l的斜率不存在，则过点E(－1,0)的直线l的方程为x＝－1，此时令A
，B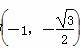
，显然|EA|＝2|EB|不成立．
若直线l的斜率存在，则设直线l的方程为y＝k(x＋1)．
则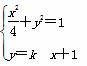
，
整理得(4k2＋1)x2＋8k2x＋4k2－4＝0.
由Δ＝(8k2)2－4(4k2＋1)(4k2－4)＝48k2＋16＞0.
设A(x1，y1)，B(x2，y2)．
故x1＋x2＝－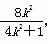
，① x1x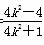2＝
.②
因为|EA|＝2|EB|，即x1＋2x2＝－3.③
①②③联立解得k＝±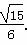
.
所以直线l的方程为
练习册系列答案
相关题目
＝1(a＞0，b＞0)与双曲线C2：
＝1有相同的渐近线，且C1的右焦点为F(
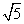，0)，则a＝________，b＝________.
表示的平面区域内存在点P(x0，y0)，满足x0－2y0＝2.求得m的取值范围是( )
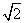，有以下四个结论：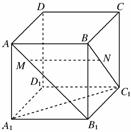
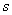的值为( )．