题目内容
函数f(x)=sinπx+cosπx+|sinπx﹣cosπx|对任意的x∈R都有f(x1)≤f(x)≤f(x2)成立,则|x2﹣x1|的最小值为( )
|
| A. |
| B. | 1 | C. | 2 | D. | 4 |
A
解:由题意,f(x)=
对任意的x∈R都有f(x1)≤f(x)≤f(x2)成立,所以f(x1)是最小值,f(x2)是最大值
|x2﹣x1|的最小值为相邻最小值与最大值处横坐标差的绝对值
由于x= 时,函数取得最大值2,x=
时,函数取得最大值2,x= 时,sinπx=cosπx=﹣
时,sinπx=cosπx=﹣ ,函数取得最小值∴|x2﹣x1|的最小值为
,函数取得最小值∴|x2﹣x1|的最小值为 =
=

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
下图表示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数m对应数轴上的点M,如图1;将线段AB围成一个圆,使两端点A、B恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图3,图3中直线AM与x轴交于点N(n,0),则 m的象就是n,记作
|
(1)方程 的解是x= ;
的解是x= ;
(2)下列说法中正确的是命题序号是 .(填出所有正确命题的序号)
① ; ②
; ②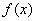 是奇函数; ③
是奇函数; ③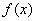 在定义域上单调递增; ④
在定义域上单调递增; ④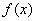 的图象关于点
的图象关于点 对称.
对称.

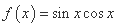 ; ②
; ②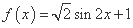 ;③
;③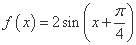 ; ④
; ④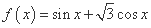 .其中“同簇函数”的是
.其中“同簇函数”的是  数
数 ,则下列说法正确的是
,则下列说法正确的是 B.当且仅当
B.当且仅当 时,
时,
 时,该函数取得最大值1D.
时,该函数取得最大值1D. 为最小正周期的周期函数
为最小正周期的周期函数 = ( )
= ( )  D.
D.
 且
且 ,则 ( )
,则 ( ) B.
B.  C.
C.  D.
D. 
 ,定义一运算:
,定义一运算: .已知
.已知 的图象上运动,且满足
的图象上运动,且满足 (其中O为坐标原点),则
(其中O为坐标原点),则 的最大值及最小正周期分别是A.
的最大值及最小正周期分别是A. B.
B. C.
C. D.
D.
 ,将
,将 的图象上各点的横坐标缩短为原来
的图象上各点的横坐标缩短为原来 ,纵坐标不变,再将所得图象向右平移
,纵坐标不变,再将所得图象向右平移 个单位,得到函数
个单位,得到函数 的图象,则函数
的图象,则函数 B.
B. C.
C. D.
D.
 .
.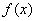 的最小正周期和对称中心;
的最小正周期和对称中心; 时,求函数
时,求函数