题目内容
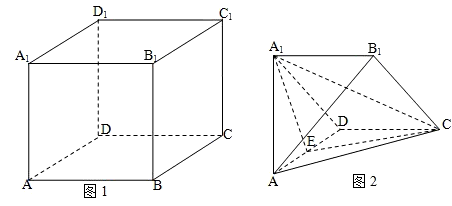 如图1,正方体ABCD-A1B1C1D1的棱长为a,E是AD的中点.现截去部分几何体后得到如图2所示的四棱锥A-A1B1CD.
如图1,正方体ABCD-A1B1C1D1的棱长为a,E是AD的中点.现截去部分几何体后得到如图2所示的四棱锥A-A1B1CD.
(Ⅰ)求四棱锥A-A1B1CD的体积;
(Ⅱ)求证:AB1∥面A1EC.
(Ⅰ)解:如图,将几何体补形成正方体,-----------------------------------------(3分)
则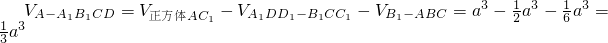 --------(7分)
--------(7分)
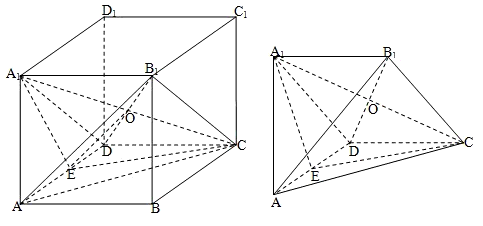
(Ⅱ)证明:在正方体AC1中,截面A1B1CD是矩形,
连接A1C,B1D,交于O,则O为B1D中点.
又E是AD的中点,连接OE,则OE是△AB1D的中位线,于是AB1∥OE,
又OE?面A1EC,A1B?面A1EC,于是AB1∥面A1EC.-------------(12分)
分析:(Ⅰ)将几何体补形成正方体,利用补形法可得结论;
(Ⅱ)连接A1C,B1D,交于O,则O为B1D中点,利用三角形中位线的性质,可得AB1∥OE,从而可得AB1∥面A1EC.
点评:本题考查四棱锥的体积.考查线面平行,解题的关键是补形,正确运用线面平行的判定.
则
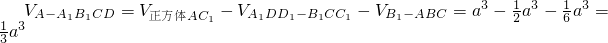 --------(7分)
--------(7分)(Ⅱ)证明:在正方体AC1中,截面A1B1CD是矩形,
连接A1C,B1D,交于O,则O为B1D中点.
又E是AD的中点,连接OE,则OE是△AB1D的中位线,于是AB1∥OE,
又OE?面A1EC,A1B?面A1EC,于是AB1∥面A1EC.-------------(12分)

分析:(Ⅰ)将几何体补形成正方体,利用补形法可得结论;
(Ⅱ)连接A1C,B1D,交于O,则O为B1D中点,利用三角形中位线的性质,可得AB1∥OE,从而可得AB1∥面A1EC.
点评:本题考查四棱锥的体积.考查线面平行,解题的关键是补形,正确运用线面平行的判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 11、如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为
11、如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,