题目内容
已知函数f(x)=(m2-m-1)x-5m-3，m为何值时，f(x)是:（1）幂函数；（2）幂函数，且是(0,+∞)上的增函数；（3）正比例函数；（4）反比例函数；（5）二次函数.
（1）m=2或m=-1.（2）m=-1.（3）m=-
.（4）m=-
.（5）m=-1
.（4）m=-.（5）m=-1（1）因f（x）是幂函数，故m2-m-1=1，即m2-m-2=0,
解得m=2或m=-1.
（2）若f（x）是幂函数且又是（0，+∞）上的增函数，
则
∴m=-1.
（3）若f(x)是正比例函数，则-5m-3=1,解得m=-,
此时m2-m-1≠0,故m=-.
（4）若f(x)是反比例函数，则-5m-3=-1,
则m=-,此时m2-m-1≠0,故m=-.
（5）若f(x)是二次函数，则-5m-3=2,即m=-1,此时m2-m-1≠0，故m=-1.
综上所述，当m=2或m=-1时，f(x)是幂函数;当m=-1时，f(x)既是幂函数，又是(0,+∞)上的增函数;
当m=-时，f(x)是正比例函数;当m=-时，f（x）是反比例函数;
当m=-1时，f（x）是二次函数.
解得m=2或m=-1.
（2）若f（x）是幂函数且又是（0，+∞）上的增函数，
则
∴m=-1.（3）若f(x)是正比例函数，则-5m-3=1,解得m=-
,此时m2-m-1≠0,故m=-
.（4）若f(x)是反比例函数，则-5m-3=-1,
则m=-
,此时m2-m-1≠0,故m=-.（5）若f(x)是二次函数，则-5m-3=2,即m=-1,此时m2-m-1≠0，故m=-1.
综上所述，当m=2或m=-1时，f(x)是幂函数;当m=-1时，f(x)既是幂函数，又是(0,+∞)上的增函数;
当m=-
时，f(x)是正比例函数;当m=-时，f（x）是反比例函数;当m=-1时，f（x）是二次函数.
练习册系列答案
相关题目
、y=
、y=
、y=
在第一象限内的图象分别是C1、C2、C3、C4,则n1、n2、n3、n4的大小关系是（ ）
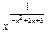（n=2k,k∈Z）的图象在［0，+∞）上单调递增，解不等式f(x2-x)＞f(x+3).
，f2(x)＝x－1，f3(x)＝x2，则f1(f2(f3(2 009)))＝__________.
、
、
满足
，
，则
的大致图象如右图，其中
（
且
）为常数，
的大致图象是（ ）
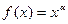的图像经过点
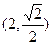，则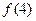
的值为（ ）
