题目内容
已知线段AB⊥平面α,BC
解析:∵![]() =
=![]() +
+![]() +
+![]() ,?
,?
∴|![]() |2=
|2=![]() ·
·![]() =(
=(![]() +
+![]() +
+![]() )·(
)·(![]() +
+![]() +
+![]() )=|
)=|![]() |2+|
|2+|![]() |2+|
|2+|![]() |2+
|2+
![]() ·
·![]() +2
+2![]() ·
·![]() +2
+2![]() ·
·![]() .①?
.①?
∵![]() =
=![]() =
=![]() =2,
=2,
∴|![]() |=|
|=|![]() |=|
|=|![]() |=2.②?
|=2.②?
又∵AB⊥α,![]()
![]() α,
α,
∴![]() ⊥
⊥![]() .∴
.∴![]() ·
·![]() =0.③?
=0.③?
CD⊥BC,∴![]() ·
·![]() =0.④?
=0.④?
把②③④代入①可得?
|![]() |2=4+4+4+2
|2=4+4+4+2![]() ·
·![]() =12+2·|
=12+2·|![]() |·|
|·|![]() |cos〈
|cos〈![]() ,
,![]() 〉=12+8·cos〈
〉=12+8·cos〈![]() ,
,![]() 〉.⑤
〉.⑤
如右图所示,过D作DF⊥α于F,连结![]() ,则∠DCF为直线
,则∠DCF为直线![]() 与α所成的角.?
与α所成的角.?

∴∠DCF=30°.
从而∠CDF=60°.
又∵![]() ⊥α,DF⊥α,∴AB∥DF.?
⊥α,DF⊥α,∴AB∥DF.?
∴〈![]() ,
,![]() 〉=〈
〉=〈![]() ,
,![]() 〉=60°.
〉=60°.
∴〈![]() ,
,![]() 〉=120°代入⑤式得到
〉=120°代入⑤式得到
|![]() |2=12+8cos120°=12-4=8.
|2=12+8cos120°=12-4=8.
∴|![]() |=2
|=2![]() .从而
.从而![]() =2
=2![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知线段AD∥平面α,且与平面α的距离为4,点B是平面α内的动点,且满足AB=5,AD=10,则B、D两点之间的距离( )
A、有最大值5
| ||||
B、有最小值
| ||||
C、有最大值5
| ||||
D、有最大值
|
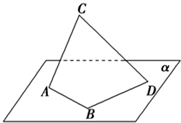 如图所示,已知线段AB,BD在平面α内,AB⊥BD,AC⊥BD,∠CAB=60°,AB=1,CA=2,BD=3,则线段CD的长为
如图所示,已知线段AB,BD在平面α内,AB⊥BD,AC⊥BD,∠CAB=60°,AB=1,CA=2,BD=3,则线段CD的长为