题目内容

已知动点P与双曲线x²-y²=1的两个焦点F₁，F₂的距离之和为定值，且cos∠F₁PF₂的最小值为 $数学公式$ ，则动点P的轨迹方程为________．

$\text{[math]}$
分析：根据椭圆定义可知，所求动点P的轨迹为以F₁，F₂为焦点的椭圆，再结合余弦定理、基本不等式，即可求出椭圆中的a，b的值．
解答：（1）∵x²-y²=1，∴c= $\text{[math]}$ ．设|PF₁|+|PF₂|=2a（常数a＞0），2a＞2c=2 $\text{[math]}$ ，∴a＞ $\text{[math]}$
由余弦定理有cos∠F₁PF₂= 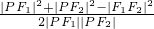$\text{[math]}$ = $\text{[math]}$ -1
∵|PF₁||PF₂|≤（ $\text{[math]}$ ）²=a²，
∴当且仅当|PF₁|=|PF₂|时，|PF₁||PF₂|取得最大值a²．
此时cos∠F₁PF₂取得最小值为 $\text{[math]}$ -1，
由题意 $\text{[math]}$ -1=- $\text{[math]}$ ，解得a²=3，
∴b²=a²-c²=3-2=1
∴P点的轨迹方程为 $\text{[math]}$ ．
故答案为： $\text{[math]}$
点评：本题考查了求轨迹方程，考查余弦定理、基本不等式的运用，考查学生的计算能力，属于中档题．

练习册系列答案

单元月考卷系列答案

小升初系统总复习指导与检测系列答案

口算达标天天练系列答案

小学毕业升学复习必做的18套试卷系列答案

小桔豆阅读与作文高效训练系列答案

总复习系统强化训练系列答案

小考宝典系列答案

高中新课程评价与检测系列答案

呼和浩特市预测卷系列答案

中考指南系列答案

相关题目

已知动点P的轨迹方程为：

=1（x＞2），O是坐标原点．
①若直线x-my-3=0截动点P的轨迹所得弦长为5，求实数m的值；
②设过P的轨迹上的点P的直线与该双曲线的两渐近线分别交于点P₁、P₂，且点P分有向线段

所成的比为λ（λ＞0），当λ∈[

已知双曲线C以x±y＝0为渐近线，且过点A(3，2)．

(1)求双曲线C的标准方程；

(2)已知动点P与双曲线C的两个焦点所连线段长的和为6，求动点P的轨迹方程．

已知双曲线C以x±y＝0为渐近线，且过点A(3，2)．

(1)求双曲线C的标准方程；

(2)已知动点P与双曲线C的两个焦点所连线段长的和为6，求动点P的轨迹方程．

设P(a,b)（b≠0）是平面直角坐标系xOy中的点，l是经过原点与点(1,b)的直线，记Q是直线l与抛物线x²＝2py（p≠0）的异于原点的交点

⑴.已知a＝1，b＝2，p＝2，求点Q的坐标。

⑵.已知点P(a,b)（ab≠0）在椭圆+y²＝1上，p＝，求证：点Q落在双曲线4x²－4y²＝1上。

⑶.已知动点P(a,b)满足ab≠0，p＝，若点Q始终落在一条关于x轴对称的抛物线上，试问动点P的轨迹落在哪种二次曲线上，并说明理由。

（上海卷理20）设P(a,b)（b≠0）是平面直角坐标系xOy中的点，l是经过原点与点(1,b)的直线，记Q是直线l与抛物线x²＝2py（p≠0）的异于原点的交点

⑴已知a＝1，b＝2，p＝2，求点Q的坐标.

⑵已知点P(a,b)（ab≠0）在椭圆+y²＝1上，p＝，求证：点Q落在双曲线4x²－4y²＝1上.

⑶已知动点P(a,b)满足ab≠0，p＝，若点Q始终落在一条关于x轴对称的抛物线上，试问动点P的轨迹落在哪种二次曲线上，并说明理由.