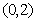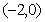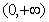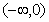题目内容
已知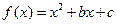 为偶函数,曲线
为偶函数,曲线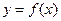 过点
过点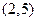 ,
,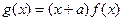 .
.
(Ⅰ)求曲线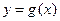 有斜率为0的切线,求实数
有斜率为0的切线,求实数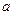 的取值范围;
的取值范围;
(Ⅱ)若当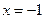 时函数
时函数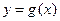 取得极值,确定
取得极值,确定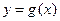 的单调区间.
的单调区间.
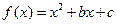 为偶函数,曲线
为偶函数,曲线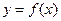 过点
过点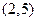 ,
,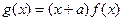 .
.(Ⅰ)求曲线
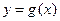 有斜率为0的切线,求实数
有斜率为0的切线,求实数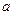 的取值范围;
的取值范围;(Ⅱ)若当
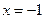 时函数
时函数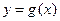 取得极值,确定
取得极值,确定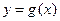 的单调区间.
的单调区间.(Ⅰ)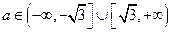 ;
;
(Ⅱ)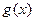 在
在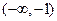 、
、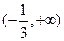 上为增函数;在
上为增函数;在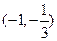 上为减函数。
上为减函数。
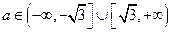 ;
;(Ⅱ)
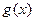 在
在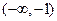 、
、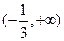 上为增函数;在
上为增函数;在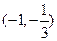 上为减函数。
上为减函数。解:(Ⅰ)
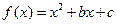 为偶函数,故
为偶函数,故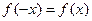 ,即有
,即有
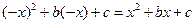 解得
解得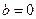 ;
;
又曲线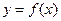 过点
过点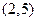 ,得
,得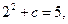 有
有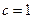
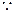
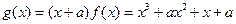 从而
从而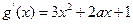 ,
,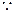 曲线
曲线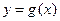 有斜率为0的切线,故有
有斜率为0的切线,故有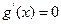 有实数解.即
有实数解.即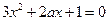 有实数解.此时有
有实数解.此时有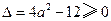 解得
解得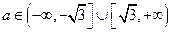 。
。
所以实数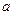 的取值范围:
的取值范围: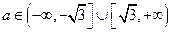 ;
;
(Ⅱ)因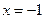 时函数
时函数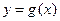 取得极值,故有
取得极值,故有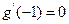 即
即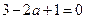 ,解得
,解得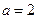
又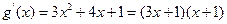 令
令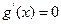 ,得
,得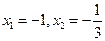
当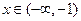 时,
时, 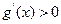 ,故
,故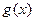 在
在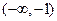 上为增函数
上为增函数
当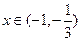 时,
时, 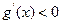 ,故
,故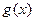 在
在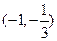 上为减函数
上为减函数
当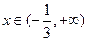 时,
时, 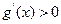 ,故
,故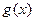 在
在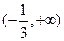 上为增函数
上为增函数
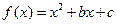 为偶函数,故
为偶函数,故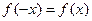 ,即有
,即有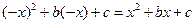 解得
解得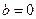 ;
;又曲线
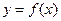 过点
过点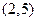 ,得
,得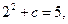 有
有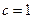
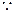
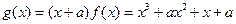 从而
从而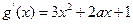 ,
,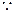 曲线
曲线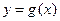 有斜率为0的切线,故有
有斜率为0的切线,故有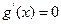 有实数解.即
有实数解.即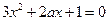 有实数解.此时有
有实数解.此时有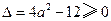 解得
解得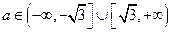 。
。所以实数
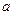 的取值范围:
的取值范围: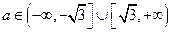 ;
;(Ⅱ)因
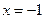 时函数
时函数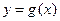 取得极值,故有
取得极值,故有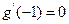 即
即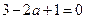 ,解得
,解得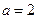
又
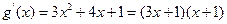 令
令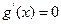 ,得
,得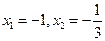
当
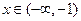 时,
时, 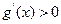 ,故
,故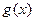 在
在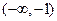 上为增函数
上为增函数当
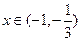 时,
时, 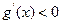 ,故
,故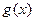 在
在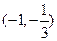 上为减函数
上为减函数当
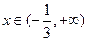 时,
时, 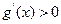 ,故
,故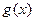 在
在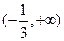 上为增函数
上为增函数
练习册系列答案
相关题目

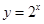
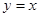
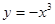
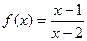 .
.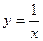 的图象平移
的图象平移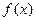 的图象,并写出交换过程;
的图象,并写出交换过程;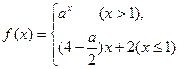 是R上的单调函数,则实数
是R上的单调函数,则实数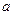 取值范围为( )
取值范围为( )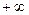 )
)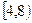
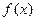 是定义在
是定义在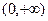 上的增函数,且对一切
上的增函数,且对一切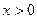 满足
满足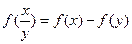 .
.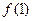 的值;
的值;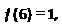 解不等式
解不等式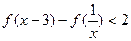 .
.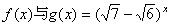 图象关于
图象关于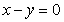 对称,则
对称,则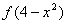 的增区间为( )
的增区间为( )