题目内容
如图所示, 、
、 分别为椭圆
分别为椭圆 :
: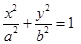
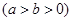 的左、右两个焦点,
的左、右两个焦点, 、
、 为两个顶点,已知顶点
为两个顶点,已知顶点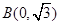 到
到 、
、 两点的距离之和为
两点的距离之和为 .
.
(1)求椭圆 的方程;
的方程;
(2)求椭圆 上任意一点
上任意一点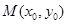 到右焦点
到右焦点 的距离的最小值;
的距离的最小值;
(3)作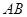 的平行线交椭圆
的平行线交椭圆 于
于 、
、 两点,求弦长
两点,求弦长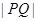 的最大值,并求
的最大值,并求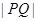 取最大值时
取最大值时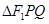 的面积.
的面积.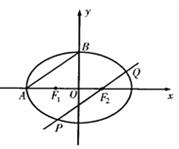
(1)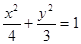 ;(2)
;(2)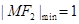 ;(3)
;(3)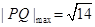 ,
, .
.
解析试题分析:(1)求椭圆方程需遵循定型、定位、定量,这里结合椭圆定义不难求得方程;(2)首先写出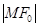 表达式然后将关于
表达式然后将关于 的二元问题转化为关于
的二元问题转化为关于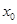 的一元问题,归结为函数求最值,注意
的一元问题,归结为函数求最值,注意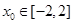 的隐含条件;(3)求直线被曲线截得的弦长是解析几何中的常见问题,求出弦长的表达式然后求最值,一般要关注判别式,否则易犯错.
的隐含条件;(3)求直线被曲线截得的弦长是解析几何中的常见问题,求出弦长的表达式然后求最值,一般要关注判别式,否则易犯错.
试题解析:(1)由已知得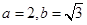 ,∴椭圆
,∴椭圆 的方程为
的方程为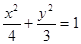 2分
2分
(2) ∵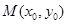 ,
,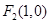 且
且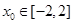 ,
,
∴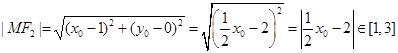 4分
4分
∴仅当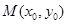 为右顶点时
为右顶点时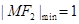 5分
5分
(3)设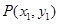 ,
,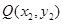 ∵
∵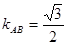 ,∴可设直线
,∴可设直线 的方程为:
的方程为: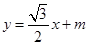 ,代入
,代入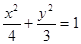 ,得
,得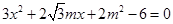 7分
7分
由韦达定理知: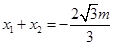 ,
,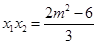 , 9分
, 9分
又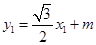 ,
,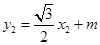
∴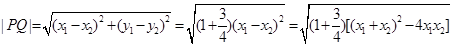
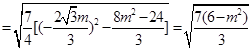
仅当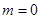 时,
时,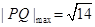 12分
12分
而此时点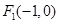 到直线
到直线 :
: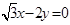 的距离
的距离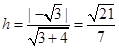 ,
,
∴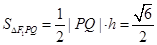 . 13分
. 13分
考点:1.椭圆方程与性质的互求;2.直线与椭圆的常规问题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
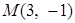 且被点
且被点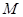 平分的双曲线
平分的双曲线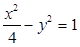 的弦所在直线方程为 _.
的弦所在直线方程为 _. ,若点P的轨迹为曲线E,过点
,若点P的轨迹为曲线E,过点  直线
直线  交曲线E于M,N两点.
交曲线E于M,N两点. MAN是一定值;
MAN是一定值; 曲线的一个焦点,并与
曲线的一个焦点,并与 ,求抛物线的方程和双曲线的方程.
,求抛物线的方程和双曲线的方程.  的对称中心为原点
的对称中心为原点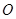 ,焦点在
,焦点在 轴上,左右焦点分别为和,且||=2,离心率
轴上,左右焦点分别为和,且||=2,离心率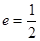 .
.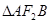 的面积为
的面积为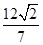 ,求直线
,求直线 的方程.
的方程.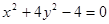 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
 .命题p: 直线l1:
.命题p: 直线l1: 与抛物线C有公共点.命题q: 直线l2:
与抛物线C有公共点.命题q: 直线l2: 被抛物线C所截得的线段长大于2.若
被抛物线C所截得的线段长大于2.若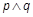 为假,
为假,  为真,求k的取值范围.
为真,求k的取值范围.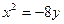 的准线方程为 .
的准线方程为 . 的焦点为F,在第一象限中过抛物线上任意一点P的切线为
的焦点为F,在第一象限中过抛物线上任意一点P的切线为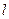 ,过P点作平行于
,过P点作平行于 轴的直线
轴的直线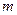 ,过焦点F作平行于
,过焦点F作平行于 ,若
,若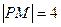 ,则点P的坐标为 .
,则点P的坐标为 .