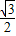题目内容
已知:a=sin85°-
cos85°,b=2(sin47°sin66°-sin24°sin43°),则a,b的大小关系为
| 3 |
a>b
a>b
.分析:利用辅助角公式对已知a,b进行化简,然后结合正弦函数y=sinx在(0,
π)单调性即可比较大小
| 1 |
| 2 |
解答:解:∵a=sin85°-
cos85°=2(
sin85°-
cos85°)
=2sin(85°-60°)=2sin25°
b=2(sin47°sin66°-sin24°sin43°)=2sin66°cos43°-sin43°cos66°
=2sin(66°-47°)=2sin19°
∵y=sinx在(0,
π)单调递增且25°>19°
∴sin25°>sin19°
∴a>b
故答案为:a>b
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=2sin(85°-60°)=2sin25°
b=2(sin47°sin66°-sin24°sin43°)=2sin66°cos43°-sin43°cos66°
=2sin(66°-47°)=2sin19°
∵y=sinx在(0,
| 1 |
| 2 |
∴sin25°>sin19°
∴a>b
故答案为:a>b
点评:本题主要考查了两角和与差的三角公式及正弦函数的单调性在比较大小中的简单应用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知向量
=(cos85°,sin85°),
=(cos25°,sin25°),则|
+
|的值为( )
| a |
| b |
| a |
| b |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
 =(cos85°,sin85°),
=(cos85°,sin85°), =(cos25°,sin25°),则|
=(cos25°,sin25°),则| +
+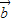 |的值为( )
|的值为( )