题目内容
【题目】如图,一个圆心角为直角的扇形![]() 花草房,半径为1,点
花草房,半径为1,点![]() 是花草房弧上一个动点,不含端点,现打算在扇形
是花草房弧上一个动点,不含端点,现打算在扇形![]() 内种花,
内种花, ![]() ,垂足为
,垂足为![]() ,
, ![]() 将扇形
将扇形![]() 分成左右两部分,在
分成左右两部分,在![]() 左侧部分三角形
左侧部分三角形![]() 为观赏区,在
为观赏区,在![]() 右侧部分种草,已知种花的单位面积的造价为
右侧部分种草,已知种花的单位面积的造价为![]() ,种草的单位面积的造价为2
,种草的单位面积的造价为2![]() ,其中
,其中![]() 为正常数,设
为正常数,设![]() ,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,总造价为
,种花的造价与种草的造价的和称为总造价,不计观赏区的造价,总造价为![]()

求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
求当![]() 为何值时,总造价最小,并求出最小值。
为何值时,总造价最小,并求出最小值。
【答案】(1)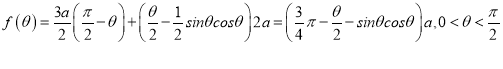 ;(2)当
;(2)当![]() 时,总造价最小,且总造价最小为
时,总造价最小,且总造价最小为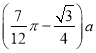 .
.
【解析】试题分析:
(1)利用题意结合图形关系可得![]() 关于
关于![]() 的函数关系式
的函数关系式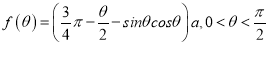 ;
;
(2)结合函数的 解析式和定义域可得当![]() 时,总造价最小,且总造价最小为
时,总造价最小,且总造价最小为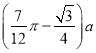 .
.
试题解析:
(1)种花区的造价为![]() ,
,
种草区的造价为![]()
故总造价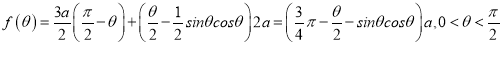 ,
,
(2)![]()
![]()
令![]() ,得到
,得到![]()
|
|
|
|
| _ | 0 | + |
| 递减 | 极小值 | 递增 |
………………………………………………………
故当![]() 时,总造价最小,且总造价最小为
时,总造价最小,且总造价最小为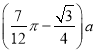 .
.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
